Использовать формулу Бернулли при достаточно большом кол-ве испытаний затруднительно. Поэтому, когда 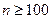 используют теорему Лапласа. Локальная теорема Лапласа: Если вер. появления соб. А в кажд. испытании постоянна и отлична от 0 и 1, то вер.
используют теорему Лапласа. Локальная теорема Лапласа: Если вер. появления соб. А в кажд. испытании постоянна и отлична от 0 и 1, то вер. 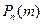 того, что соб. А появится в n испытаниях ровно m раз, приближен. равна(тем точнее, чем больше n) значению функции:
того, что соб. А появится в n испытаниях ровно m раз, приближен. равна(тем точнее, чем больше n) значению функции: 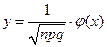 , где
, где  , где
, где 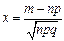 . Имеются таблицы, в кот. помещены значения функц.
. Имеются таблицы, в кот. помещены значения функц. 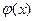 , соответствующ. положит. значениям аргумента
, соответствующ. положит. значениям аргумента 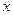 . Для отрицат. значений аргумента пользуются теми же таблицами, т.к. функц.
. Для отрицат. значений аргумента пользуются теми же таблицами, т.к. функц. 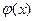 четная, т.е.
четная, т.е. 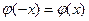 . Вер. того, что соб. А появится в n испытаниях ровно m раз
. Вер. того, что соб. А появится в n испытаниях ровно m раз 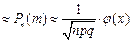 , где
, где 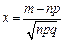 . Предположим, что производится n испытаний, в кажд. из кот. вер. появл. соб. А постоянна и равна p,
. Предположим, что производится n испытаний, в кажд. из кот. вер. появл. соб. А постоянна и равна p, 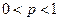 . Нужно найти вер того, что соб. А появится в n испытаниях не менее
. Нужно найти вер того, что соб. А появится в n испытаниях не менее 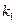 и не более
и не более 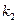 раз, т.е. нужно найти
раз, т.е. нужно найти 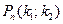 . Теор.: Если вер. P наступления события в кажд. испытании постоянна и отлична от 0 и 1, то вер.
. Теор.: Если вер. P наступления события в кажд. испытании постоянна и отлична от 0 и 1, то вер. 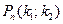 того, что в n испытаниях соб. А появится от
того, что в n испытаниях соб. А появится от 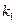 до
до 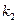 раз
раз 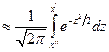 , где
, где 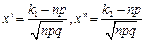 . При решении задач, требующ. применения интегральн. теоремы Лапласа, пользуются специальн. таблицами. В них даны значения функции
. При решении задач, требующ. применения интегральн. теоремы Лапласа, пользуются специальн. таблицами. В них даны значения функции 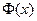 для положит. значений аргумента
для положит. значений аргумента 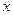 . Для
. Для 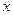 <0 функц.
<0 функц. 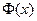 нечетн., т.е.
нечетн., т.е. 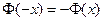 . В табл. приведены значения для
. В табл. приведены значения для 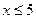 . При
. При 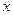 >5 значение функц. считается постоян. и равно 0,5. Для того, чтобы можно было использовать табл. функций Лапл. преобразуем последнюю формулу:
>5 значение функц. считается постоян. и равно 0,5. Для того, чтобы можно было использовать табл. функций Лапл. преобразуем последнюю формулу: 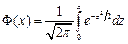 ;
; 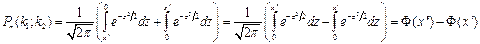 , где
, где 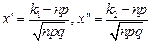 . Вер. того, что соб. А появится в n независим. испытаниях от
. Вер. того, что соб. А появится в n независим. испытаниях от 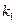 до
до 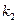 раз равна
раз равна 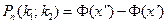 .
.