Если вер. события p в отдельн. испытании близка к 0, то даже при большом числе испытаний n, но небольш. величине 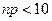 вероятности
вероятности 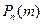 , получен. по локальн. формуле Лапл. не достаточно близки к их истин. значениям. В таких случаях применяют формулу Пуасона. Теор.: Если вер. p наступления соб. А в кажд. испытании постоянна, но близка к 0, число независим. испытаний n достаточн. велико, а
, получен. по локальн. формуле Лапл. не достаточно близки к их истин. значениям. В таких случаях применяют формулу Пуасона. Теор.: Если вер. p наступления соб. А в кажд. испытании постоянна, но близка к 0, число независим. испытаний n достаточн. велико, а 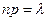 , то вер.
, то вер. 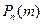 того, что в n независ. испытаниях соб. А наступит m раз
того, что в n независ. испытаниях соб. А наступит m раз 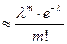 . Это формула Пуасона. Доказ-во: Для вычисления вер.
. Это формула Пуасона. Доказ-во: Для вычисления вер. 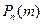 воспользуемся формул. Бернулли:
воспользуемся формул. Бернулли: 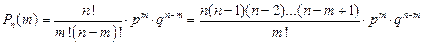 (Т.к.
(Т.к. 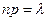 ,то
,то 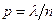 )=
)= 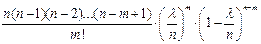 . Т.к. по условию n велико, то найдем предел правой части последн. равенства при
. Т.к. по условию n велико, то найдем предел правой части последн. равенства при 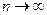 , при этом будет получено приближен. значение вероятн.:
, при этом будет получено приближен. значение вероятн.: 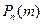 =
= 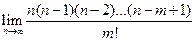
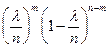 =
= 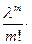
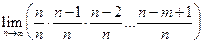

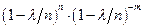 =
= 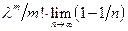
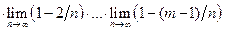
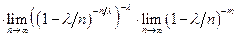 =
= 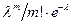 Пределы всех скобок, кроме предпоследн. равны 1 при
Пределы всех скобок, кроме предпоследн. равны 1 при 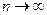 . Следоват-но вер. того, что в n испытаниях событие появится m раз
. Следоват-но вер. того, что в n испытаниях событие появится m раз 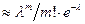 . Замечание: Формулу Пуассона обычно используют, когда
. Замечание: Формулу Пуассона обычно используют, когда 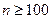 , а
, а 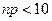 .
.