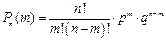При решении вероятностн. задач часто приходится сталкиваться с ситуациями, в кот. одно и тоже испытание повторяется многократно. В рез-те каждого опыта может появиться или не появиться некотор. соб. А, причем нас интересует не рез-т каждого отдельного опыта, а общее число появлений соб. А в рез-те серии опытов. Модель рассматрив. ситуации выглядит след. образом: проводится n испытаний, в каждом из кот. соб. А может произойти или нет. Причем вероятность события в кажд. отдельн. испытании постоянна, т.е. не меняется от испытания к испытанию. Требуется определить вер. m появлений соб. А в n испытаниях. Подобн. задачи решаются довольно легко, если испытания явл. независимыми. Опред.: Неск-ко испытаний назыв. независим. относит-но соб. А, если вер. соб. А в кажд. из них не зависит от исходов др. испытаний. Напр, неск-ко последоват. бросаний монет представляют собой независим. опыты. Производится n независим. опытов, в кажд. из кот. может появиться или не появ. некотор. соб.А. Вер. появл. данного события в кажд. опыте постоянна и равна p, а вер. непоявления=q. Требуется найти вер. Pn(m) того, что соб. А в этих n опытах появится m раз. Рассмотрим событие Bm, состоящ. в том, что соб. А появится в этих n опытах ровно m раз. Разложим соб. Bm на сумму произведен. событий, состоящих в появлении или непоявл. соб. А в определ. опыте. Каждый вар-т появл. соб. Bm должен состоять из m появлений соб. А или n-m непоявл. соб. А. Bm=А1А2…Аm 
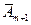
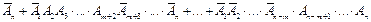 Каждое произведен. соб. А должно происходить m раз, а
Каждое произведен. соб. А должно происходить m раз, а 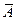 n-m раз. Число всех комбинаций такого рода равно
n-m раз. Число всех комбинаций такого рода равно  , т.е. равно числу способов, какими можно из n опытов выбрать m, в кот. произошло соб. А. Вер. каждой такой комбинации по теор. умножен. для независ. событий равна
, т.е. равно числу способов, какими можно из n опытов выбрать m, в кот. произошло соб. А. Вер. каждой такой комбинации по теор. умножен. для независ. событий равна 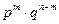 . Т.к. комбинации между собой несовместны, то по теор. сложения вер. соб. Bm равна
. Т.к. комбинации между собой несовместны, то по теор. сложения вер. соб. Bm равна 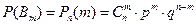 . Т.о., если производится n независим. опытов, в кажд. из кот. соб. А появляется с вер. p, то вер. того, что соб. А появится ровно m раз, выражается формулой
. Т.о., если производится n независим. опытов, в кажд. из кот. соб. А появляется с вер. p, то вер. того, что соб. А появится ровно m раз, выражается формулой 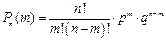


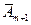
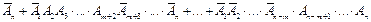 Каждое произведен. соб. А должно происходить m раз, а
Каждое произведен. соб. А должно происходить m раз, а 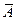 n-m раз. Число всех комбинаций такого рода равно
n-m раз. Число всех комбинаций такого рода равно  , т.е. равно числу способов, какими можно из n опытов выбрать m, в кот. произошло соб. А. Вер. каждой такой комбинации по теор. умножен. для независ. событий равна
, т.е. равно числу способов, какими можно из n опытов выбрать m, в кот. произошло соб. А. Вер. каждой такой комбинации по теор. умножен. для независ. событий равна 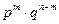 . Т.к. комбинации между собой несовместны, то по теор. сложения вер. соб. Bm равна
. Т.к. комбинации между собой несовместны, то по теор. сложения вер. соб. Bm равна 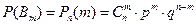 . Т.о., если производится n независим. опытов, в кажд. из кот. соб. А появляется с вер. p, то вер. того, что соб. А появится ровно m раз, выражается формулой
. Т.о., если производится n независим. опытов, в кажд. из кот. соб. А появляется с вер. p, то вер. того, что соб. А появится ровно m раз, выражается формулой