Появление тех или иных значений случ. величины можно рассматривать как события, а различн. событиям соответств. различн. вероятности. Поэтому возможн. значения случ. величины различаются между собой с вероятностн. точки зрения. Перечисление всех возм. значений случ. вел. не дает достаточно полн. представл. о ней. Кроме значений случ. вел. необходимо знать, как часто м. появляться те или иные значения случ. вел. в рез-те испытаний проводящихся в одинак. условиях. Рассмотрим дискретн. случ. вел. X, возможн. значения кот. 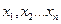 . Кажд. из этих значений возможно, но не достоверно, и случ. вел. X м. принять кажд. из них с некотор. вероятностью. В рез-те опыта вел. X примет одно их этих значений:
. Кажд. из этих значений возможно, но не достоверно, и случ. вел. X м. принять кажд. из них с некотор. вероятностью. В рез-те опыта вел. X примет одно их этих значений: 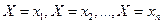 , т.е. произойдет одно из полной группы несовместн. событие. Обозначим вероятн. этих событий:
, т.е. произойдет одно из полной группы несовместн. событие. Обозначим вероятн. этих событий:  . Т.к. указан. события несовметны и образуют полн. группу, то
. Т.к. указан. события несовметны и образуют полн. группу, то  , т.е. сумма вероятностей всех возм. значений равна 1.Если мн-во значений случ. вел. образует бесконечн., но счетн. мн-во, то ряд
, т.е. сумма вероятностей всех возм. значений равна 1.Если мн-во значений случ. вел. образует бесконечн., но счетн. мн-во, то ряд  сходится и его сумма равна 1. Т.о. суммарная вер. единицы распределена между отдельн. значениями СВ. СВ будет полностью описана с вероятн. точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вер. обладает каждое из событий. Опред.: Законом распредел. СВ назыв. всякое соотношение, устанавливающ. связь между возможн. значениями СВ и соответсв. им вероятностями. Закон распредел. м. задать табличным, графич. или аналитич. способами. При табличн. способе 1-ая строка табл. содержит возможн. значение СВ, а 2-ая соответств. вероятности. Обычно зачение СВ располагают в возрастающ. порядке. Чтобы придать ряду распредел. более наглядн. вид часто прибегают к его графич. изображению. По оси абсцисс откладывают возможн. знач. СВ, а по оси ординат вероятности этих значений. Получен. точки соединяют отрезками прямых. Получен. фигуру называют многоугольн. распредел. Он полностью характеризует СВ и является одной из форм закона распред. Замеч.: Ряд распред. и многоуг. распред. можно построить только для дискретн. СВ
сходится и его сумма равна 1. Т.о. суммарная вер. единицы распределена между отдельн. значениями СВ. СВ будет полностью описана с вероятн. точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вер. обладает каждое из событий. Опред.: Законом распредел. СВ назыв. всякое соотношение, устанавливающ. связь между возможн. значениями СВ и соответсв. им вероятностями. Закон распредел. м. задать табличным, графич. или аналитич. способами. При табличн. способе 1-ая строка табл. содержит возможн. значение СВ, а 2-ая соответств. вероятности. Обычно зачение СВ располагают в возрастающ. порядке. Чтобы придать ряду распредел. более наглядн. вид часто прибегают к его графич. изображению. По оси абсцисс откладывают возможн. знач. СВ, а по оси ординат вероятности этих значений. Получен. точки соединяют отрезками прямых. Получен. фигуру называют многоугольн. распредел. Он полностью характеризует СВ и является одной из форм закона распред. Замеч.: Ряд распред. и многоуг. распред. можно построить только для дискретн. СВ

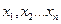 . Кажд. из этих значений возможно, но не достоверно, и случ. вел. X м. принять кажд. из них с некотор. вероятностью. В рез-те опыта вел. X примет одно их этих значений:
. Кажд. из этих значений возможно, но не достоверно, и случ. вел. X м. принять кажд. из них с некотор. вероятностью. В рез-те опыта вел. X примет одно их этих значений: 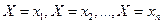 , т.е. произойдет одно из полной группы несовместн. событие. Обозначим вероятн. этих событий:
, т.е. произойдет одно из полной группы несовместн. событие. Обозначим вероятн. этих событий:  . Т.к. указан. события несовметны и образуют полн. группу, то
. Т.к. указан. события несовметны и образуют полн. группу, то  , т.е. сумма вероятностей всех возм. значений равна 1.Если мн-во значений случ. вел. образует бесконечн., но счетн. мн-во, то ряд
, т.е. сумма вероятностей всех возм. значений равна 1.Если мн-во значений случ. вел. образует бесконечн., но счетн. мн-во, то ряд  сходится и его сумма равна 1. Т.о. суммарная вер. единицы распределена между отдельн. значениями СВ. СВ будет полностью описана с вероятн. точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вер. обладает каждое из событий. Опред.: Законом распредел. СВ назыв. всякое соотношение, устанавливающ. связь между возможн. значениями СВ и соответсв. им вероятностями. Закон распредел. м. задать табличным, графич. или аналитич. способами. При табличн. способе 1-ая строка табл. содержит возможн. значение СВ, а 2-ая соответств. вероятности. Обычно зачение СВ располагают в возрастающ. порядке. Чтобы придать ряду распредел. более наглядн. вид часто прибегают к его графич. изображению. По оси абсцисс откладывают возможн. знач. СВ, а по оси ординат вероятности этих значений. Получен. точки соединяют отрезками прямых. Получен. фигуру называют многоугольн. распредел. Он полностью характеризует СВ и является одной из форм закона распред. Замеч.: Ряд распред. и многоуг. распред. можно построить только для дискретн. СВ
сходится и его сумма равна 1. Т.о. суммарная вер. единицы распределена между отдельн. значениями СВ. СВ будет полностью описана с вероятн. точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вер. обладает каждое из событий. Опред.: Законом распредел. СВ назыв. всякое соотношение, устанавливающ. связь между возможн. значениями СВ и соответсв. им вероятностями. Закон распредел. м. задать табличным, графич. или аналитич. способами. При табличн. способе 1-ая строка табл. содержит возможн. значение СВ, а 2-ая соответств. вероятности. Обычно зачение СВ располагают в возрастающ. порядке. Чтобы придать ряду распредел. более наглядн. вид часто прибегают к его графич. изображению. По оси абсцисс откладывают возможн. знач. СВ, а по оси ординат вероятности этих значений. Получен. точки соединяют отрезками прямых. Получен. фигуру называют многоугольн. распредел. Он полностью характеризует СВ и является одной из форм закона распред. Замеч.: Ряд распред. и многоуг. распред. можно построить только для дискретн. СВ


