Ряд распредел. не явл. исчерпывающ. хар-кой для СВ, т.к. он существ. только для дискретн. СВ. Непрерывн. СВ имеет бесчислен. мн-во возможн. значений, сплошь заполняющ. некотор. промежуток. Составить табл., в кот. были бы перечислены все возможн. значения СВ невозможно. Кроме того в дальнейшем будет показано, что кажд. отдельн. значение обладает нулевой вер. Однако несмотря на рав-во 0-вых вероятностей отдельн. значений непрерывн. СВ, нахождение ее возможн. значений в различн. интервалах обладает различн. и отличными от 0 вероятностями. Т.о. для непрер. СВ, так же как и для дискретн., можно определить закон распредел., но в неск-ко ином виде. Для хар-ки поведения непрер. СВ целесообразно использовать не вер. события X=x, а вер. соб. X<x, где x – некотор. действит. число. Вер. P(X<x) явл. функцией аргумента x. Будем обозначать эту функц. F(x). Опред.: Функцией распред. СВ X назыв. функц. F(x), задающая вер. того, что СВ X принимает значение меньшее x, т.е. F(x)=P(X<x). Функц. распред. F(x) назыв. также интегральн. функцией распред. или интегральн. законом распредел. Функц. распред. существует для всех СВ(как дискретн., так и непрерывн.).Она полностью характеризует СВ величину с вероятн. точки зрения, т.е. явл. одной из форм закона распредел. Функц. распредел. допускает простую геометрич. интерпретацию. Рассмотрим СВ X как случ. точку на оси OX, кот. в рез-те опыта м. занять то или иное положение. Пусть на оси OX выбрана конкретн. точка x, тогда в рез-те опыта случ. точка X м. оказаться левее или правее точки x. Вер. того, что случ. точка X оказалась левее точки x и будет являться функц. распредел., зависит от положения точки x. Для дискретн. СВ, кот. может принимать значение 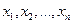 , функц. распредел. имеет вид
, функц. распредел. имеет вид  , где нер-во
, где нер-во 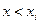 означает, что суммирование касается всех тех знач.
означает, что суммирование касается всех тех знач.  , величина кот. <x. Предположим, аргумент x принял какое-то определ. знач., но такое, что выполняется нер-во
, величина кот. <x. Предположим, аргумент x принял какое-то определ. знач., но такое, что выполняется нер-во 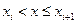 , тогда левее числа x на числов. оси окажутся только те знач. СВ, кот. имеют индекс 1,2,3…,i. Поэтому нер-во X<x выполняется, если велич. X примет знач.
, тогда левее числа x на числов. оси окажутся только те знач. СВ, кот. имеют индекс 1,2,3…,i. Поэтому нер-во X<x выполняется, если велич. X примет знач.  , где k=1,2,3…,i. Т.о. событие X<x наступит, если наступит любое из соб.
, где k=1,2,3…,i. Т.о. событие X<x наступит, если наступит любое из соб.  ,
,  ,…,
,…,  . Т.к. эти соб. несовмест., то по теор. сложен. вер. P(X<x)=
. Т.к. эти соб. несовмест., то по теор. сложен. вер. P(X<x)=  +
+  +…+
+…+ 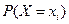 =
=  . Построим ряд распредел. дискретн. СВ Х:
. Построим ряд распредел. дискретн. СВ Х:
| Х
| x1
| x2
| …
| xi
| …
| xn
|
| p
| p1
| p2
| …
| pi
| …
| pn
|
При  , F(x)=
, F(x)= 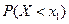 =0; При
=0; При  , F(x)=
, F(x)=  =
= 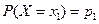 ; при
; при  , F(x)=
, F(x)= 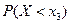 =
= 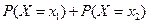 =
=  ; при
; при  , F(x)=
, F(x)=  =
= 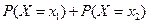 +
+  ; при
; при  , F(x)=
, F(x)=  =
= 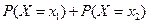 +…+
+…+ 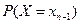 =
=  ; при
; при  , F(x)=
, F(x)= 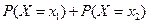 +…+
+…+  =
=  . Для дискретн. СВ график функции распредел. представл. собой разрывную ступенчатую фигуру. Когда перемен. х проходит через какое-ниб. из возможн. знач. СВ, знач. функц. распредел. меняется скачкообразно,т.е. функц. имеет скачок в тех точках, в кот. случ. величина принимает конкретн. знач. согласно ряду распредел., причем величина скачка равна вер. этого значения. Замеч.: По функц. распредел. дискретн. СВ всегда можно восстановить ее ряд распредел. Св-ва функц. распредел.: 1) если F(x) –функц. распредел. СВ Х, то
. Для дискретн. СВ график функции распредел. представл. собой разрывную ступенчатую фигуру. Когда перемен. х проходит через какое-ниб. из возможн. знач. СВ, знач. функц. распредел. меняется скачкообразно,т.е. функц. имеет скачок в тех точках, в кот. случ. величина принимает конкретн. знач. согласно ряду распредел., причем величина скачка равна вер. этого значения. Замеч.: По функц. распредел. дискретн. СВ всегда можно восстановить ее ряд распредел. Св-ва функц. распредел.: 1) если F(x) –функц. распредел. СВ Х, то 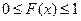 для всех х. Это св-во вытекает из определ. функции распредел.; 2) F(x) явл. неубывающей, т.е.
для всех х. Это св-во вытекает из определ. функции распредел.; 2) F(x) явл. неубывающей, т.е. 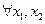 при
при  ,
,  . Доказ-во: Пусть
. Доказ-во: Пусть 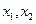 - точки числ. оси, причем
- точки числ. оси, причем 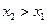 . Покажем, что
. Покажем, что  . Рассмотрим 2 несовместн. события: соб.А состоит в том, что
. Рассмотрим 2 несовместн. события: соб.А состоит в том, что 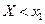 , а соб. В сост. в том, что
, а соб. В сост. в том, что  . Тогда соб. А+В =
. Тогда соб. А+В = 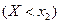 . По теор. сложен. вер. P(A+B)=P(A)+P(B) или P(X<
. По теор. сложен. вер. P(A+B)=P(A)+P(B) или P(X< 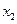 )= P(X<
)= P(X< 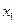 )+P(
)+P( ). Используя определ. функц. распредел. получаем F(
). Используя определ. функц. распредел. получаем F(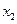 )=F(
)=F(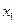 )+ P(
)+ P( ). Т.к. вер. того, что (
). Т.к. вер. того, что ( )
) 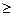 0, то F(
0, то F(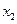 )
) 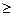 F(
F(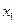 ), т.е. F(x) – неубывающ. функция; 3) если F(x) – функц. распредел., то
), т.е. F(x) – неубывающ. функция; 3) если F(x) – функц. распредел., то  =0,
=0,  =1. Доказ-во: Т.к. F(x) – монотон. функция и ограниченная(из св-ва 1), то
=1. Доказ-во: Т.к. F(x) – монотон. функция и ограниченная(из св-ва 1), то 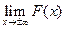 существует. В силу предполагаем. непрерывности F(x) можно записать, что
существует. В силу предполагаем. непрерывности F(x) можно записать, что  =
= 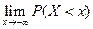 =
= 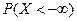 . Т.к. соб.
. Т.к. соб.  невозможное, то его вер.=0. Значит
невозможное, то его вер.=0. Значит  =0. Аналогично
=0. Аналогично  =
= 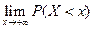 =
= 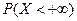 . Соб.
. Соб. 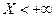 - достоверное, а его вер. =1. Значит
- достоверное, а его вер. =1. Значит  =1.
=1.

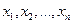 , функц. распредел. имеет вид
, функц. распредел. имеет вид  , где нер-во
, где нер-во 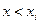 означает, что суммирование касается всех тех знач.
означает, что суммирование касается всех тех знач.  , величина кот. <x. Предположим, аргумент x принял какое-то определ. знач., но такое, что выполняется нер-во
, величина кот. <x. Предположим, аргумент x принял какое-то определ. знач., но такое, что выполняется нер-во 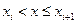 , тогда левее числа x на числов. оси окажутся только те знач. СВ, кот. имеют индекс 1,2,3…,i. Поэтому нер-во X<x выполняется, если велич. X примет знач.
, тогда левее числа x на числов. оси окажутся только те знач. СВ, кот. имеют индекс 1,2,3…,i. Поэтому нер-во X<x выполняется, если велич. X примет знач.  , где k=1,2,3…,i. Т.о. событие X<x наступит, если наступит любое из соб.
, где k=1,2,3…,i. Т.о. событие X<x наступит, если наступит любое из соб.  ,
,  ,…,
,…,  . Т.к. эти соб. несовмест., то по теор. сложен. вер. P(X<x)=
. Т.к. эти соб. несовмест., то по теор. сложен. вер. P(X<x)=  +
+  +…+
+…+ 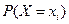 =
=  . Построим ряд распредел. дискретн. СВ Х:
. Построим ряд распредел. дискретн. СВ Х: , F(x)=
, F(x)= 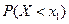 =0; При
=0; При  , F(x)=
, F(x)=  =
= 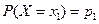 ; при
; при  , F(x)=
, F(x)= 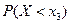 =
= 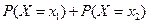 =
=  ; при
; при  , F(x)=
, F(x)=  =
=  ; при
; при  , F(x)=
, F(x)=  =
= 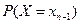 =
=  ; при
; при  , F(x)=
, F(x)=  =
=  . Для дискретн. СВ график функции распредел. представл. собой разрывную ступенчатую фигуру. Когда перемен. х проходит через какое-ниб. из возможн. знач. СВ, знач. функц. распредел. меняется скачкообразно,т.е. функц. имеет скачок в тех точках, в кот. случ. величина принимает конкретн. знач. согласно ряду распредел., причем величина скачка равна вер. этого значения. Замеч.: По функц. распредел. дискретн. СВ всегда можно восстановить ее ряд распредел. Св-ва функц. распредел.: 1) если F(x) –функц. распредел. СВ Х, то
. Для дискретн. СВ график функции распредел. представл. собой разрывную ступенчатую фигуру. Когда перемен. х проходит через какое-ниб. из возможн. знач. СВ, знач. функц. распредел. меняется скачкообразно,т.е. функц. имеет скачок в тех точках, в кот. случ. величина принимает конкретн. знач. согласно ряду распредел., причем величина скачка равна вер. этого значения. Замеч.: По функц. распредел. дискретн. СВ всегда можно восстановить ее ряд распредел. Св-ва функц. распредел.: 1) если F(x) –функц. распредел. СВ Х, то 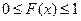 для всех х. Это св-во вытекает из определ. функции распредел.; 2) F(x) явл. неубывающей, т.е.
для всех х. Это св-во вытекает из определ. функции распредел.; 2) F(x) явл. неубывающей, т.е. 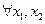 при
при  ,
,  . Доказ-во: Пусть
. Доказ-во: Пусть 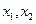 - точки числ. оси, причем
- точки числ. оси, причем 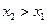 . Покажем, что
. Покажем, что  . Рассмотрим 2 несовместн. события: соб.А состоит в том, что
. Рассмотрим 2 несовместн. события: соб.А состоит в том, что 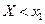 , а соб. В сост. в том, что
, а соб. В сост. в том, что  . Тогда соб. А+В =
. Тогда соб. А+В = 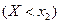 . По теор. сложен. вер. P(A+B)=P(A)+P(B) или P(X<
. По теор. сложен. вер. P(A+B)=P(A)+P(B) или P(X< 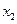 )= P(X<
)= P(X< 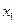 )+P(
)+P( ). Используя определ. функц. распредел. получаем F(
). Используя определ. функц. распредел. получаем F(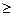 0, то F(
0, то F( =0,
=0,  =1. Доказ-во: Т.к. F(x) – монотон. функция и ограниченная(из св-ва 1), то
=1. Доказ-во: Т.к. F(x) – монотон. функция и ограниченная(из св-ва 1), то 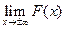 существует. В силу предполагаем. непрерывности F(x) можно записать, что
существует. В силу предполагаем. непрерывности F(x) можно записать, что 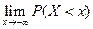 =
= 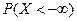 . Т.к. соб.
. Т.к. соб.  невозможное, то его вер.=0. Значит
невозможное, то его вер.=0. Значит 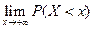 =
= 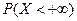 . Соб.
. Соб. 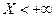 - достоверное, а его вер. =1. Значит
- достоверное, а его вер. =1. Значит 


