Спектральные представления как частный случай геометрических методов в теории сигналов.
Историческая заслуга в разработке спектральных представлений (гармонического анализа) принадлежит Жану Б. Фурье. В современной трактовке спектральные разложения могут быть представлены как частный случай геометрических методов в теории сигналов (из функционального анализа).
Иными словами, возникает идея представления функций неким набором элементарных, в каком-то смысле “перпендикулярных”, функций, так, как это делается в геометрии с векторами. Впервые такое разложение было сделано Фурье. Он предложил непрерывную в интервале
где
Если базисный набор функций определён, то аппроксимируемая функция
Ортогональность базисных функций математически записывается в виде равенства нулю их скалярных произведений. Если в интервале
Норма базисной функции записывается в виде интеграла:
Нормированность функций:
В целом:
Выполнение условий (7), (8) или (9) обеспечивает систему (ортонормированную) базисных функций или просто базис. Если условие нормированности не выполняется, то нормируют функции делением на норму. Фурье предложил в качестве идеальных математических моделей взять гармонический ряд sin и cos.
Определение коэффициентов ряда Фурье (6) (6) – обобщенный ряд Фурье. Образуем скалярное воспроизведение базисной и аппроксимируемой функций:
Получим:
Чтобы найти коэффициент гармонического разложения, нужно вычислить скалярное произведение аппроксимируемой функции и члена ортонормированного базиса с тем же коэффициентом. Аппроксимация периодических функций тригонометрическим рядом Наиболее популярными являются базисные функции в виде элементарных тригонометрических функций и экспоненциальных, потому что они инвариантны к производимым над ними операциям линейными стационарными операторами. В частности – к операциям интегрирования и дифференцирования. Пусть n = 0, 1, 2… T – период. Ортонормированным базисом для таких функций служит следующий ряд:
где
Примечание: если взять
Аппроксимация периодической функции по базису (11) выглядит:
где Формулы (13) получены по процедуре (10). Примечание: если исходная функция четная, то коэффициенты bi = 0; если нечетная, то ai = 0.
Представить тригонометрическим рядом Фурье повторяющиеся с периодом T видеоимпульсы прямоугольной формы длительностью τи, симметричные относительно начала координат. Решение. Находим коэффициенты:
где
|

 Возникает естественная геометрическая аналогия: если вектор представляется через его проекции в прямоугольной системе координат, если можно определить по проекциям ряд характеристик, в том числе важнейшую – модуль вектора (длину, иначе, норму), то почему бы не поступить так же и с сигналами? И сигнал представлять через элементарные сигналы, входящие в ортогональный базис, а количественной характеристикой для сравнения их между собой взять ту же норму, определив ее соответствующим образом.
Возникает естественная геометрическая аналогия: если вектор представляется через его проекции в прямоугольной системе координат, если можно определить по проекциям ряд характеристик, в том числе важнейшую – модуль вектора (длину, иначе, норму), то почему бы не поступить так же и с сигналами? И сигнал представлять через элементарные сигналы, входящие в ортогональный базис, а количественной характеристикой для сравнения их между собой взять ту же норму, определив ее соответствующим образом.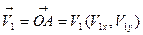 ,
,
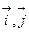 - единичные векторы (орты)
- единичные векторы (орты)
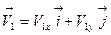
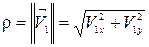 - длина вектора (норма)
- длина вектора (норма)


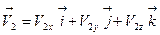
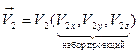
 функцию времени
функцию времени  представить в виде ряда:
представить в виде ряда: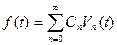 , (6)
, (6)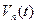
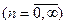 - некий базисный набор элементарных функций, которые являются ортогональными в указанном интервале и нормированными (их норма равна 1);
- некий базисный набор элементарных функций, которые являются ортогональными в указанном интервале и нормированными (их норма равна 1);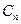 - коэффициенты ряда Фурье, коэффициенты веса.
- коэффициенты ряда Фурье, коэффициенты веса.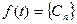 .
.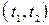 каждая из базисных функций ортогональна, то
каждая из базисных функций ортогональна, то (7)
(7)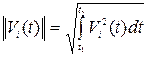 условие нормировки
условие нормировки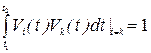 (8)
(8)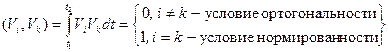 (9)
(9)
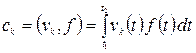 (10)
(10)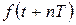 – периодическая функция.
– периодическая функция.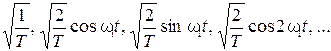 (11)
(11)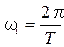 – основная гармоника;
– основная гармоника;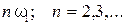 – высшие гармоники;
– высшие гармоники;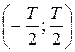 – интервал ортонормированности.
– интервал ортонормированности.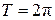 , то получим вариант базисного ряда:
, то получим вариант базисного ряда: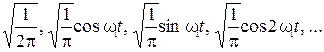
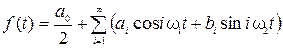 , (12)
, (12)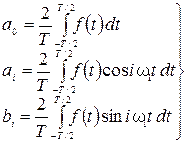 (13)
(13) Задача № 1
Задача № 1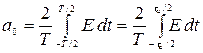
 ,
,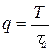 – скважность импульса.
– скважность импульса.
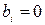 , так как функция четная.
, так как функция четная.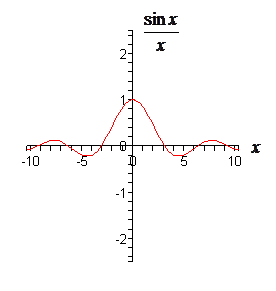

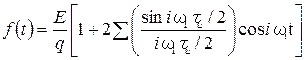 (14)
(14)


