Спектральный анализ непериодических (импульсных) сигналов.
Идея разложения импульсного сигнала состоит в том, чтобы мысленно дополнить его такими же сигналами и представить периодическим с периодом T
Воспользуемся комплексной формой ряда Фурье (17), (18)
Заменим
При
(*) представляется в виде пары преобразований
(19) – спектральная плотность, получаемая прямым преобразованием Фурье
(20) – обратное преобразование Фурье (19) и (20) являются фундаментальными формулами в теории сигналов. Физический смысл спектральной плотности состоит в том, что она показывает распределение амплитуд сплошного спектра непериодического сигнала по частотам:
Примечание: Можно ли применить понятие спектральной плотности к периодическим сигналам в неинтегрируемом сигнале? Можно, если ввести описание через обобщенные функции времени, к которым относятся функции Хевисайда или Дирака.
Задача 1. Найти
Задача 2. Спектральная плотность экспоненциального видеоимпульса.
Задача 3.
(**) – фильтрующее свойство
|
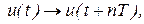при этом можно воспользоваться одним из вариантов ряда Фурье. Затем, устремив 
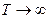, оставить на оси лишь одиночный импульс и этот же переход осуществить с преобразованием Фурье: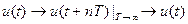
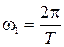при 
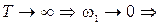в этом случае спектр одиночного импульса становится сплошным.
на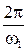 
, 
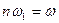(дискретная частота 
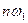превращается в текущую частоту 
).
(*)
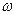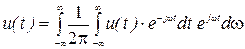
(19)
(20)
.
видеоимпульса прямоугольной формы высотой E.
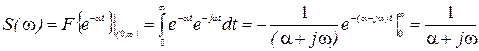, т.е. спектральная плотность может быть величиной комплексной.
.
(**)
.
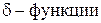(21) - фильтрующее свойство 
