Основные свойства преобразования Фурье.
Применяют краткие обозначения взаимосоответствия сигнала во времени и его изображения Фурье.
1. Обладает линейностью:
2. Свойство вещественной и мнимой частей спектральной плотности Заменим в (19) экспоненту по формуле Эйлера:
Подставим этот результат в (20), где также заменим экспоненту формулой Эйлера:
Известно что интеграл в симметричных приделах от нечетной функции =0, поэтому для уничтожения мнимой компоненты сигнала, нужно сохранить нечетность 2-х подинтегралных выражений,и в связи с этим, реальная часть спектральной плотности должна быть четной, а мнимая часть – нечетной (22). Итак 3. Теорема запаздывания (сдвиг функции во времени): Если Доказательство:
ч.т.д. 4. Теорема смещения (смещение спектра): Если Доказывается аналогично пункту 3.
5. Изменение масштаба сигнала.
Из (24) следует что, чем уже импульсный сигнал тем шире его спектр и наоборот. 6. Спектральная плотность произведения сигналов (теорема о свертке). Пусть имеем 2 сигнала со спектрами:
Найдем:
Заменим v(t) через обратное преобразование Фурье:
Интеграл в выражении
Таким образом:
Спектральная плотность произведения 2-х сигналов равна с точностью до коэффициента (1/2π) свертке спектральных плотностей сомножителей. 7. Обобщенная формула Рэлея (равенство Парсеваля). Пусть имеются 2 сигнала с известными спектральными плотностями, и в общем случае – комплексно-значимые.
Образуем скалярное произведение этих сигналов и определим спектральную плотность.
Заменим
Комментарий к (26): скалярное произведение 2-х сигналов равно с точностью до множителя (1/2π) скалярному произведению их спектральных плотностей. Это важное свойство используется для получения спектров неинтегрируемых сигналов. 8. Спектральная плотность производной сигнала. Пусть
Преобразование Фурье – линейная операция. Применим ее к формуле
Так как
Спектральная плотность производной получается домножением спектральной плотности сигнала на оператор дифференцирования в комплексной области j ω.
|

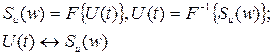
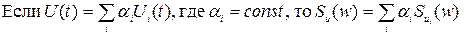
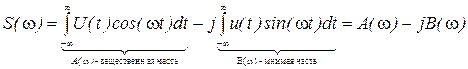 .
. (***)
(***)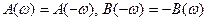 (22)
(22) , то
, то 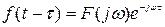 (23)
(23)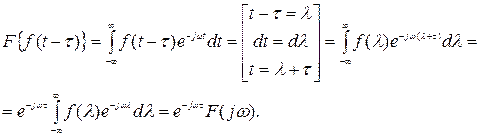
 , то
, то  .
.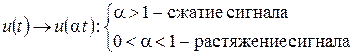
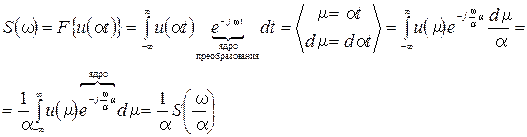
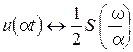 (24)
(24)
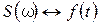
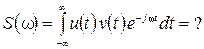


 называется сверткой спектральной плотности, и обозначается:
называется сверткой спектральной плотности, и обозначается:
 (25)
(25)
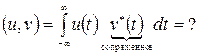
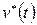 через F -1.
через F -1.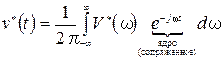
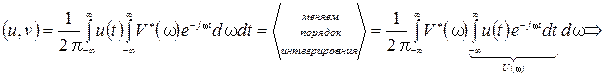
 (26)
(26)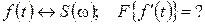
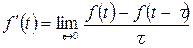

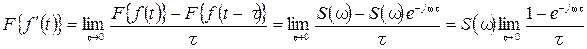
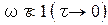 , разложим в ряд Маклорена:
, разложим в ряд Маклорена: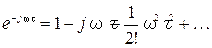


 (28)
(28)


