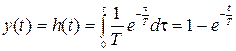Получение формулы динамического представления сигнала.
(По рисунку б). Каждый отдельный прямоугольный импульс можно описать с помощью функции Хэвисайда. Очевидно, что импульс высотой
Очевидно, вся аппроксимируемая функция
Используем формальный приём: умножаем (2) и делим (2) на
Пусть
Пояснение. Рассмотрим следующую функцию, вычисляемую через функцию Хэвисайда:
Ее площадь всегда равна 1, а предел при
Окончательно:
или, если
Комментарий к формулам (3) и (4). Получено представление функции времени через идеализированный математический объект – замечательную Нетрудно видеть, что в этом случае реакцию на произвольный сигнал получим суммированием реакций на бесконечную последовательность смещенных δ-импульсов с площадями, равными текущей высоте входного сигнала (эта сумма переходит в интеграл):
Для общности:
Пусть весовая функция:
На вход такого звена поступает единичное входное воздействие необходимо найти реакцию на выходе, в этом случае выходной сигнал называется переходная функция
|

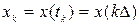 и длительностью
и длительностью 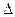 , возникающий в момент
, возникающий в момент  :
: (1)
(1) является суммой подобных импульсов:
является суммой подобных импульсов: (2)
(2)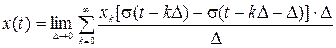
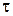 - новый (текущий) аргумент интегрирования, т.е.
- новый (текущий) аргумент интегрирования, т.е.  . Суммирование заменится интегрированием,
. Суммирование заменится интегрированием, 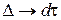 , а предел отношения равен:
, а предел отношения равен: .
. . (*)
. (*) определяет δ-функцию, т.е.
определяет δ-функцию, т.е. (**)
(**) (3)
(3) является чётной, поэтому возможна запись:
является чётной, поэтому возможна запись: (4)
(4) , получим
, получим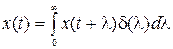 .
.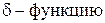 Дирака. Это представление играет фундаментальную роль в теории линейных систем и с его помощью можно определять реакцию динамической системы на входной сигнал произвольного вида. Из теории известно, что реакцией динамической системы на входную
Дирака. Это представление играет фундаментальную роль в теории линейных систем и с его помощью можно определять реакцию динамической системы на входной сигнал произвольного вида. Из теории известно, что реакцией динамической системы на входную 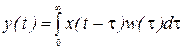 (5) – формула Дюамеля
(5) – формула Дюамеля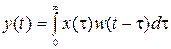
 .
. - импульсно переходная функция или весовая функция.
- импульсно переходная функция или весовая функция. , где Т-постоянная времени.
, где Т-постоянная времени.