Решение интегрального уравнения методом вспомогательного фильтра.
Название такого метода решения – метод вспомогательного фильтра, метод выбеливания, метод предискажения. Характеристика фильтра выбирается заранее и он зависит от свойств ядра интегрального выражения, и для второго звена решается такая же задача оптимизации, но при условии, что на входе белый шум. Очевидно интегральное уравнение для второго звена выглядит так же, как (10), только записывается для искаженных сигналов: Уравнение 2-ого звена
Здесь æ2(τ)=L-1{H2(p)} Интеграл в правой части равен =
Задача принципиально решена. Остаётся лишь рассмотреть методику выбора фильтра и подставить в (12) исходные данные. Примечание: интегральные уравнения (10), (11) являются необходимыми условиями минимума функционала и в то же время достаточными, ибо ухудшать систему можно беспредельно и максимум погрешности находится в бесконечности.
|


 æ2(τ;)
æ2(τ;) 
 (11)
(11)
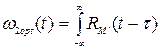 æ2(τ;)
æ2(τ;)  (12)
(12)


