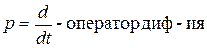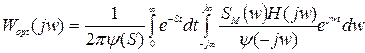Получение оптимальной характеристики всей системы в целом.
Исходный материал формулы (***), (11), (12) и структурная схема. Перейдём в оптимальном решении (12) к исходным данным. Предварительно заменим корреляционную функцию на спектральную плотность через обратное преобразование Фурье. Заменим:
Имеем:
Найдём оптимальную передаточную функцию второго звена прямым преобразованием Фурье от (15):
Оптимальная передаточная функция всей системы равна:
где (17)- оптимальное решение вид Калмогорова Варианты записи оптимального решения в квадратурах: 1. Вариант (17) в частотной области 2. Заменим
3. Смешанная форма записи:
Внутренние интегралы берутся с помощью вычетов, а внешние – напрямую.
Задача На вход курсового радиоприёмника системы посадки (измеряется отклонение от плоскости курса) поступает случайный полезный сигнал с корреляционной функцией и помеха в виде белого шума. Система должна обеспечить упреждающую информацию экипажу о будущем отклонении на такт вперёд. Необходимо определить физически реализуемую передаточную функцию по критерию минимума СКО.
|


 æ2(τ)dτ;=
æ2(τ)dτ;= 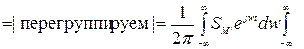 æ2(τ)dτ=
æ2(τ)dτ=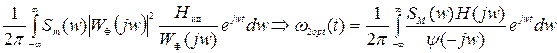 (15)
(15)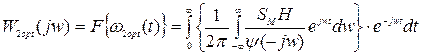 (16)
(16)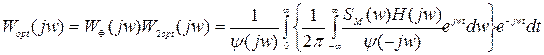 (17)
(17) - факторизация.
- факторизация.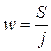 , тогда
, тогда 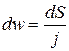 ,
,