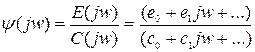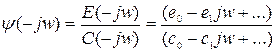Анализ свойств ядра интегрального уравнения
Им является суммарное корреляционная функция, анализ удобно проводить в частотной области. Определим спектральную плотность Sφ(w)
Например
В общем виде
если В связи с тем, что полиномы А и В зависят от квадрата частоты, нули и полюсы являются комплексносопряженными и имеют квадратную симметрию располагающейся на комплексной плоскости.
Рассмотрим
Образуем к. АЧХ
Полюсы:
Рассмотренный пример показывает, что при работе с характеристиками в виде коэффициента передачи мощности (квадрат АЧХ) мы получаем зеркальные нули и полюсы, находящиеся в полуплоскости неустойчивых решений, и на самом деле исходная характеристика имеет только устойчивые нули и полюсы. В связи с этим обстоятельством Боде и Шеннон предложили для получения устойчивых передаточных функций оставлять, как и положено, только левые нули и полюсы на плоскости p, и спектральной плотности случайных сигналов представлять в виде 2-х сомножителей, одни из которых содержат нули и полюсы в области устойчивой, а вторые – не устойчивой. Такая операция разбиения спектральной плотности называется факторизацией. Если собрать нули и полюсы спектральной плотности в разных плоскостях мы получим полиномы с действительными коэффициентами.
Согласно (13) спектральную плотность можно представить в виде произведения 2-х дробно-рациональных функций, имеющих нули и полюсы в двух полуплоскостях, т. е. факторизовать.
Свойства ядра интегрального ядра такова, что соответствующую спектральную плотность можно факторизовать.
|

 - дробно-рациональная функция от квадратной частоты.
- дробно-рациональная функция от квадратной частоты.
 или
или 
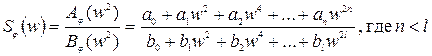
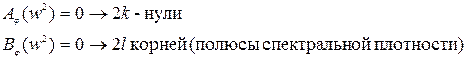


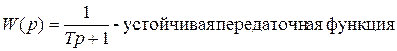




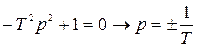

 если p=jw
если p=jw (13)
(13)