Получение выражения для СКО в виде функционала от искомой весовой функции
Подставлять непосредственно (5) в (6) нельзя: лишимся общности результата (не получим общий результат). Надо заменить операцию возведения в квадрат (6) умножим (5) на такое же выражение, но с другим аргументом интегрирования: например, с σ.
Раскроем скобки и перемножим. Получим 25 слагаемых. Рассмотрим некоторые из них. 1) Меняем порядок интегрирования:
2) рассмотрим 25-е слагаемое:
Остальные 23 слагаемых рассматриваются также. При этом будут получаться взаимокорреляционные функции RMN, RNM, RMu * и т.д. Примем для простоты, что взаимокорреляции нет и эти функции равны 0. Окончательно, выражение для СКО примет вид:
где Комментарий: СКО (7) является функционалом, потому что значение этой ошибки зависит от выбора неизвестной функции ω(t). Минимизацией функционалов занимается теория вариационного исчисления.
|

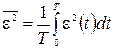 (6) – СКО
(6) – СКО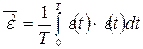
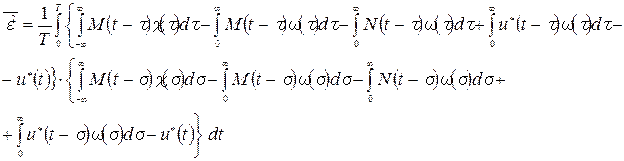
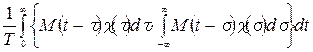 .
.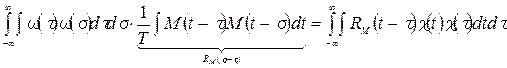 .
. – дисперсия случайного процесса
– дисперсия случайного процесса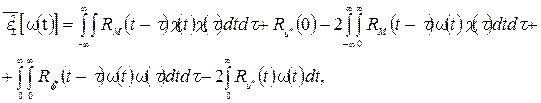 (7)
(7)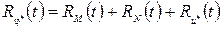 (8)
(8)


