Определение оптимальных параметров при заданной структуре фильтра (измерительного устройства).
Подобные задачи решаются минимизацией выражения для СКО. Решение: 1)
2) Из приложений в учебниках и задачниках по ТАУ:
Вариант:
Подгоним наше выражение для
В итоге
Очевидно, степень полинома в знаменателе будет равна трём, и нам необходимо подогнать выражение под следующий табличный интеграл:
Подгоняем интеграл Знаменатель:
Числитель:
3) Комментарий к решенным задачам: главная особенность состоит в определении оптимальных параметров по заранее заданной структуре или схеме. А что если сами структуры не оптимальны? Приходим к следующей идее: искать целиком оптимальную передаточную функцию или весовую функцию, которая обеспечивала бы минимум СКО. Впервые такую задачу по синтезу оптимальной передаточной функции поставил Винер в середине прошлого века. Решение, полученное им, независимо от него получено Колмогоровым. Примечание: когда ищется функция, доставляющая экстремум (минимум) критерию качества (в нашем случае критерий качества – это СКО), то говорят, что задан функционал:
Минимизацией функционалов занимается теория вариационного исчисления (Бернулли).
|
- она же 
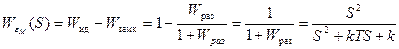- передаточная функция по ошибке воспроизведения полезного сигнала.
.
.
.
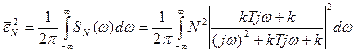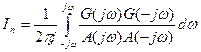под табличный интеграл:
.
.
.
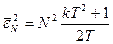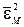под табличный I 3, для этого 
перемножим с трёхчленом знаменателя:
.
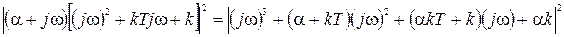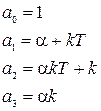
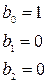
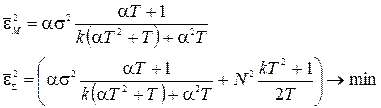
– функционал.
