Корреляционный и спектральный анализ случайных процессов.
Детерминированный процесс новой информации не несёт. Информация заключается в случайном процессе.
Если Ансамбль реализаций случайного процесса:
Случайные процессы описываются вероятностными законами (функции распределения, которые бывают интегральные и дифференциальные).
Для полного описания случайного процесса необходим
В инженерной практике неудобно пользоваться вероятностными законами, а желательно иметь числовые характеристики, неслучайные характеристики. Очевидно, это должны быть некие осреднённые величины. Их называют моментами (моменты 1-ого, 2-ого и т.д. порядка, смешанные, центральные моменты). Для инженерной практики оказалось достаточным использовать только три такие характеристики: математическое ожидание (среднее значение), дисперсия, корреляционная функция. Кроме того, оказалось плодотворным понятие стационарного случайного процесса. Стационарный случайный процесс – это процесс, у которого моменты первого порядка от времени не зависят (математическое ожидание, дисперсия), а корреляционная функция зависит не от двух аргументов времени, а от расстояния между сечениями, т.е. от разности аргументов. Математическое ожидание стационарного процесса, получаемая осреднением по множеству реализаций:
Работать с формулами, подобными (*), т.е. средними, неудобно. Оказалось, что большинство процессов подчиняются эргодической гипотезе, которая означает, что неслучайные характеристики, получаемые осреднением по множеству реализаций, равны подобным характеристикам, получаемым осреднением по времени из одной достаточно длительной реализации.
Физический смысл дисперсии: она характеризует меру рассеяния реализации процесса около среднего значения (геометрический смысл) и характеризует мощность этих флуктуаций (колебаний) – физический смысл. Корреляция – связь, взаимозависимость, поэтому корреляционная функция случайного процесса характеризует степень связи двух сечений случайного процесса: чем больше она, тем легче можно предсказать второе значение по первому базовому. С математической точки зрения, это операция взятия математического ожидания от произведения двух значений случайного процесса:
Корреляционная функция центрированного процесса:
Примечание: в связи с большим удобством анализа сигналов в частотной области введено понятие спектральной плотности как прямого преобразования Фурье от корреляционной функции:
Смысл этой спектральной плотности: характеризует распределение по частотам не энергии сигнала, а мощности, или распределение дисперсии:
Основное свойство корреляционной функции – чётность
Если ядро преобразования заменим по формуле Эйлера Формулы Винера-Хинчина:
|

 - случайная функция.
- случайная функция. , то
, то 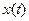 - случайный процесс.
- случайный процесс.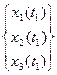 - сечения случайного процесса.
- сечения случайного процесса. - одномерный интегральный закон распределения.
- одномерный интегральный закон распределения. - дифференциальный закон (плотность вероятности).
- дифференциальный закон (плотность вероятности). - закон нормировки.
- закон нормировки.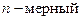 закон:
закон: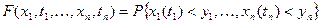
 .
. (*)
(*) (44)
(44)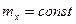 для стационарных процессов.
для стационарных процессов. (45)
(45) (46)
(46) (47)
(47) по (47)
по (47) (48)
(48) (49)
(49)
 и подставим в (48) и (49), то вследствие чётности функции интегралы от
и подставим в (48) и (49), то вследствие чётности функции интегралы от 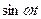 в симметричных пределах будут равны нулю.
в симметричных пределах будут равны нулю.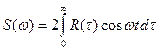 , (50)
, (50) . (51)
. (51)


