Взаимокорреляционная функция
Она отражает меру связи между двумя процессами, между двумя сигналами, один из которых смещен.
Из сравнения (35) и (39) можно сделать выводы: 1. автокорреляционная функция является нечетной;
2. автокорреляционная функция в нуле имеет максимум. Это энергия сигнала;
3. взаимокорреляционная функция может быть нечетной; 4. максимум взаимокорреляционной функции может быть и не в нуле.
Связь между корреляционной функцией сигнала и спектральной плотностью энергии (энергетическим спектром) Рассмотрим автокорреляционную функцию по определению и заменим в нем первый сомножитель на обратное преобразование Фурье от спектральной плотности.
В итоге:
В формуле (40):
Комментарий: выражение (41) называется спектральной плотностью энергии сигнала и в отличие от ранее рассмотренной спектральной плотности имеет смысл распределение по частотам не амплитуд гармоник, а энергии сигнала. Кратко называется – энергетический спектр. Таким образом, корреляционная функция представляет собою обратное преобразование Фурье от энергетического спектра.
Естественно, существует и прямое преобразование Фурье от корреляционной функции. Это и будет энергетический спектр.
(42) и (43) имеют фундаментальное значение в теории сигналов. В частности из них следует, что чем шире энергетический спектр, тем уже интервал корреляции, и наоборот. На практике из экспериментальных данных находят корреляционную функцию (аппроксимируют), а по ней вычисляют спектральную плотность энергии.
|

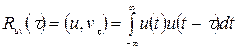 (39)
(39)


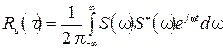 (40)
(40) (41)
(41) (42)
(42)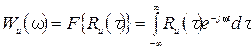 (43)
(43)


