Погрешности при случайных сигналах
Если
Если Пусть
Очевидно, спектральная плотность ошибки в этом случае на выходе равна:
Следовательно, ошибка на выходе:
Работать с этой формулой нельзя. Ошибка на выходе оценивается осредненной величиной или средним квадратом ошибки (либо СКО):
Рассмотрим корреляционную функцию в нуле:
Практическая формула вычисления Рассмотрим
Следовательно,
Комментарий: средний квадрат ошибки на выходе получается интегрированием соответствующих спектральных плотностей ошибок. Такие интегралы в комплексной области вычислены для инженерного применения и имеются в справочной литературе (до порядка n = 7).
|
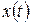трактовать как входную случайную помеху 
, то согласно (53) можем найти спектральную плотность наведенной на выходе погрешности от этой помехи:
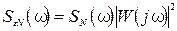(54)
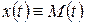– случайный полезный сигнал. Тогда возникает ошибка из-за возникновения полезного сигнала:
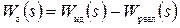(55)
(56)
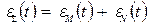
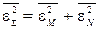– средний квадрат ошибки (57)
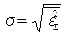– СКО
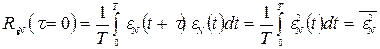
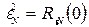(58)
через обратное преобразование Фурье: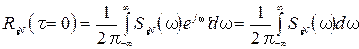
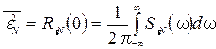(59)
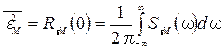(60)
