Основные формулы из теории вариационного исчисления.1) Необходимые условия минимума функционала: вариация функционала должна быть равна нулю.
(в матанализе: Дифференциал функции:
Тогда при
2) “Рабочие” формулы вычисления дифференциала функции и вариации функционала:
где Доказательство:
Вариация функционала:
где
3) Основная лемма вариационного исчисления: если равен нулю интеграл следующего вида
|
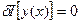(а)
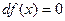или 
).
, причем 
при 
.
.
, (б)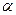
- “рабочий” параметр
(ч.т.д.)
, (в)
- приращение аргумента функционала;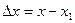
- приращение аргумента функции;
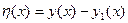- приращение аргумента функционала.
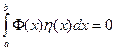при любом выборе 
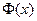- непрерывна в 
, то должно быть 
. (г)
