Получение необходимого условия минимума СКО.
В выражении (7) первые два слагаемых при подстановке исходных данных будут конкретным числом и не влияют на определение точки экстремума, поэтому их можно выбросить и минимизировать усеченное выражение для СКО:
Вычислим вариацию функционала. Для этого в начале вычислим функционал от аргумента с приращением.
Применим к (**) рабочую формулу (в)
Преобразуем (V) под основную лемму вариационного исчисления η(t) – «пробная»функция.
Согласно основной лемме
Неизвестная весовая функция входит под знак интеграла, следовательно (10) является интегральным уравнением Винера-Колмогорова и относится к классическим интегральным уравнениям Фредгольма первого рода. Коэффициент при неизвестной функции является ядром интегрального выражения как является суммарная корреляционная функция. Решение интегрального выражения зависит от свойств ядра. В отличии от диф. исчисления теория решения интегральных уравнений разрабатывается лишь для некоторых их классов. Решение 10 основывается на эвристическом приеме. Он состоит в том что ядро упрощается до Не трудно понять, что искажающий фильтр должен быть выбран так чтобы суммарный входной сигнал превратить в белый шум. Примечание: Необходимое условие минимума (10) является и достаточным условием минимума. Доказать это можно 2-мя способами: 1) Логический. Ухудшать систему можно беспредельно и погрешность будет 2) Математический. Для этого нужно доказать, что функция от аргумента с приращением
|

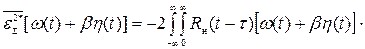 æ(τ;)
æ(τ;) 

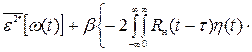 æ(τ;)
æ(τ;) 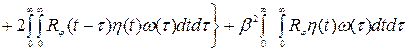 (**)
(**)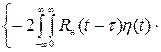 æ(τ;)
æ(τ;) 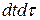


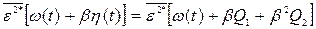
 (9)
(9)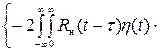 æ(τ;)
æ(τ;) 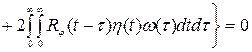 (V)
(V)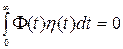
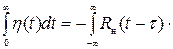 æ(τ;)
æ(τ;) 


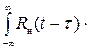 æ(τ;)
æ(τ;) 
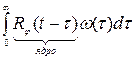 (10)
(10)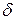 - функции. Специально вводимым искусственным фильтром, а интегралы с
- функции. Специально вводимым искусственным фильтром, а интегралы с 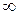 . Поэтому найденное условие (10) является минимальным, а не максимальным.
. Поэтому найденное условие (10) является минимальным, а не максимальным.



