Получение алгебраической формы оптимального решения методом Ли-Юк-Вина
Идея решения этим методом базируется на том свойстве оригиналов и изображений по Лапласу, что если оригинал равен нулю на одной из полуосей времени, то изображение не содержит нулей и полюсов в соответствующей полуплоскости. Образуем из интегрального уравнения (14) функцию времени:
(29) выполняется при
Тогда изображение этой функции q (t) не должно содержать нулей и полюсов в верхней полуплоскости.
Преобразуем правую часть (29) по Фурье:
Факторизуем спектральную плотность:
и поделим обе части (30) на
Указание: разобьем 2-е слагаемое (31) на сумму 2-х слагаемых. Одно из них содержит нули и полюсы в верхней полуплоскости, другое – в нижней.
Это операция носит название сепарации. Очевидно, в (32) слагаемые 1-е и 2-е должны взаимно уничтожиться, чтобы не было нулей и полюсов в верхней полуплоскости.
Примечание: оптимальное решение (33) справедливо только для идеальных операторов в виде так называемого обобщенного оператора воспроизведения, представляющего собой степенной полином:
Только в этом случае возможно проведение сепарации.
Задача. Спроектировать оптимальный фильтр при следующих исходных данных:
Решаем по (38) без учета внутренней помехи
где
1) Факторизация:
|

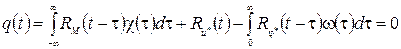 (29)
(29)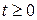 .
.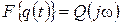
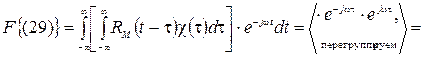
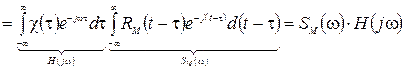
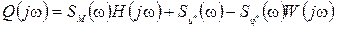 (30)
(30)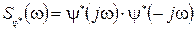
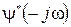 :
: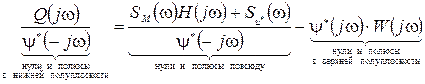
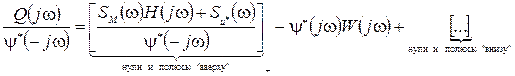 (32)
(32)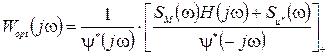 (33)
(33)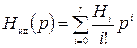 (34)
(34)
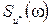 . Это фильтр Винера-Колмогорова.
. Это фильтр Винера-Колмогорова.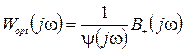 , (35)
, (35)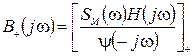 (36)
(36)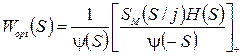 .
.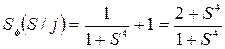 (метод неопределенных коэффициентов)
(метод неопределенных коэффициентов)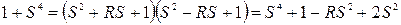
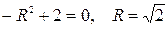 .
.


