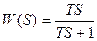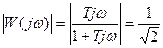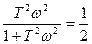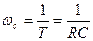Синтез линейных фильтров по заданной АЧХ.Исходные данные для синтеза могут быть сформулированы из требований ТЗ, а также по результатам решения теоретической задачи оптимального синтеза.
Самый лучший вариант характеристики – это комплексный коэффициент передачи мощности, который равен, как известно, квадрату модуля комплексного коэффициента передачи, иначе квадрату модуля комплексной передаточной функции: Надеженй решать
Пусть даны Идеальная прямоугольная АЧХ нереализуема, поэтому её аппроксимируют подходящими полиномами: полиномами Баттерворта и Чебышева. По признаку пропускания на выход входных сигналов на определённых частотах, а также их подавления (задерживания, заграждения) различают фильтры:
Частота среза определяется по уровню спада АЧХ (по соглашению в измерительной технике допускается спад АЧХ на 10%, а в электротехнике спад АЧХ до значения 0.707). Задача. Найти нижнюю границу полосы пропускания при спаде АЧХ на
Решение:
|
В последнем случае может быть получено оптимальное решение, трудно поддающееся реализации и которое в дальнейшем потребуется аппроксимировать с целью упрощения. Для инженерной практики наиболее удобным вариантом синтеза является именно аппроксимация подходящим полиномом некой исходной идеальной характеристики. Так как на рисунке спектры перекрываются то на выходе появится наведенная погрешность в этом случае, когда спектры перекрываются надежней решать задачу Винера – Колмагорова на синтез оптимального фильтра - это обеспечит минимальную погрешность на выходе.
.
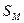и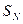 
.
.
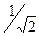