Математическая модель сигнала на одном периоде повторенияНа одном периоде повторения аналитическая запись сигнала выглядит следующим образом:
где
циклическая частота следования –
Скважность заданного периодического сигнала
где длительность импульса
function s = cosinob1(t,Um,T,Uo) % s = cosinob1(t,Um,T,Uo) % t - вектор текущего времени % Um - амплитуда % T - период косинусоиды % Uo - уровень отсечки
if nargin == 1 Um = 1; T = 1; Uo = 0; elseif nargin == 2 T =1; Uo = 0; elseif nargin == 3 Uo =0; end teta = acos(Uo/Um); t1 = teta*T/(2*pi); n = length(t); s = zeros(1,n); for i=1:n if abs(t(i)) <= T/2 if abs(t(i)) < t1 s(i)=-Uo+Um*cos(2*pi*t(i)/T); end end end
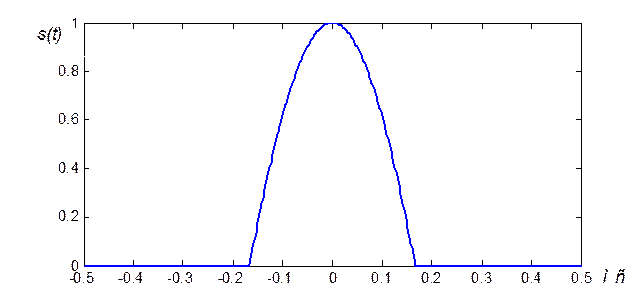
Для того, чтобы вычислить значения сигнала в 1024 точках на одном периоде повторения, следует ввести команды: T = 1e-3; Um = 2; Uo = 1; t = linspace(-T/2,T/2*1023/1024, 1024); s1 = cosinob1(t,Um,T,Uo); plot(t,s1)
Рис. 1.3. Исследуемый сигнал на одном периоде повторения
|
(2.1)
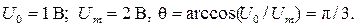Период сигнала задан и равен T= 1 мс. Величина 
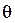называется углом отсечки. Круговая частота следования 
определяется по формуле
, (2.2)
(2.3)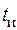
определяется его областью существования (
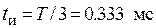). Сигнал на одном периоде повторения, рассчитанный по формуле (2.1), представлен на рис. 2.3. Текст m -файла cosinobn, реализующего формулу (2.1), приведён ниже.
