Сигнал как аналитическая функция
Сигнал представляется в виде математического соотношения, в котором устанавливается связь между переменной, которой сопоставлено свойство сигнал, и конечным набором других переменных (свойств), которые называются параметры сигнала. Например, в непрерывном гармоническом колебании При моделировании такого сигнала в системе MATLAB как некоторого объекта, устанавливающего непрерывную связь между параметрами сигнала и его значением, можно использовать следующие варианты: 1. Представление сигнала в виде команды в командной строке. Сначала в рабочее пространство вносятся фиксированные значения параметров: Uo = 1; f = 10; theta = 0; далее задаётся набор точек, в которых (или которой) сигнал должен быть вычислен: t = 0:0.01:1; а потом по команде xt = Uo*sin(2*pi*f*t+theta); в рабочем пространстве появляется соответствующий набор значений сигнала.
2. Представление сигнала в виде строки. Если заданы параметры сигнала, т.е. все переменные в его аналитическом выражении, то это выражение можно записать сначала в форме строки s = 'Uo*sin(2*pi*f*t+theta)'; а затем вычислять одно или несколько его значений с помощью xs = eval(s);
3. Представление сигнала в виде встроенной строки. Такое представление – нечто среднее между представлением сигнала просто строкой и m- функцией, поскольку в этом случае при вычислении сигнала его параметры можно задавать как входные переменные. Сначала записывается встроенная строка (inline-объект) y = inline('sin(2*pi*f*t + theta)','t', 'f', 'theta') результат выполнения которой отображается в виде формы обращения к функции: Inline function: y(t,f,theta) = sin(2*pi*f*t + theta) Значения сигнала определяются при выполнении команды обращения, например, xg = y(t, f, 0);
4. Представление сигнала в виде m- функции. Это наиболее универсальный и часто используемый вид задания сигналов. Поскольку в системе MATLAB можно использовать переменное количество входных (nargin) и выходных (nargout) параметров, то некоторые из них могут при вызове m- функции опускаться:
function y = sinf(t,f,theta) % y = sinf(t,f,theta) % y = sinf(2*pi*f*t + theta) if nargin = = 3 y = sinf(2*pi*f*t + theta); elseif nargin = = 2 y = sinf(2*pi*f*t); end
Вычисление значений сигнала для заданного набора параметров выполняется по команде xf = sinf(t, f, theta); или, например, по команде xf = sinf(t, 10);
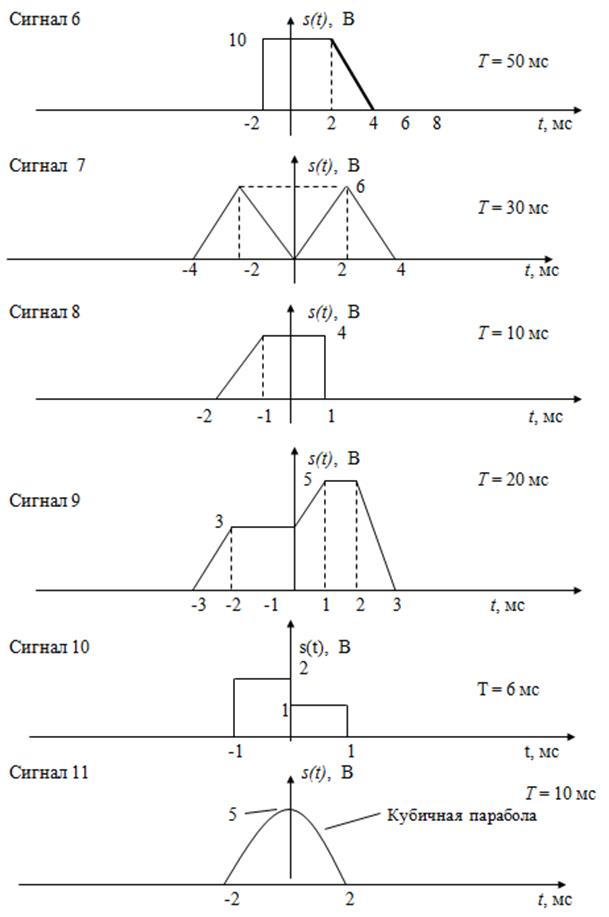
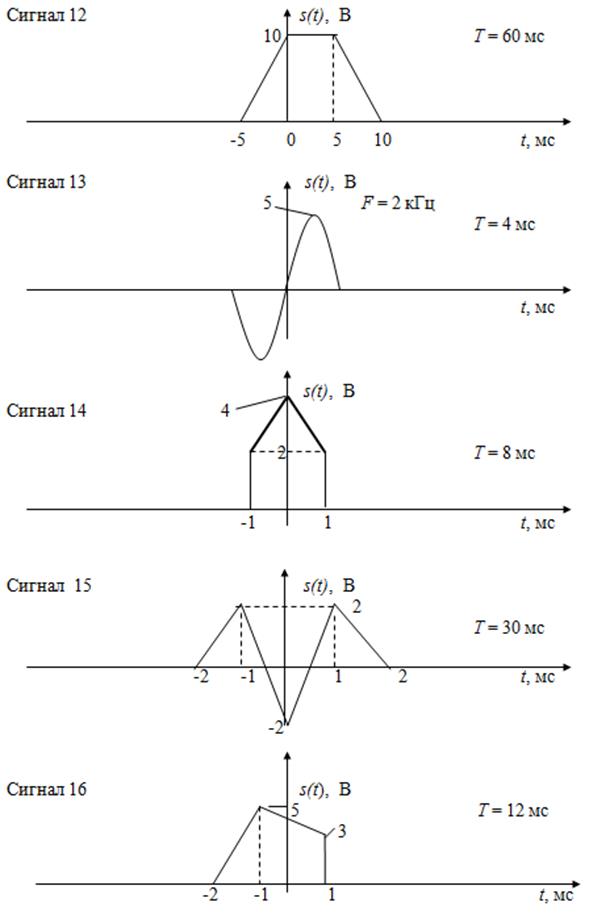
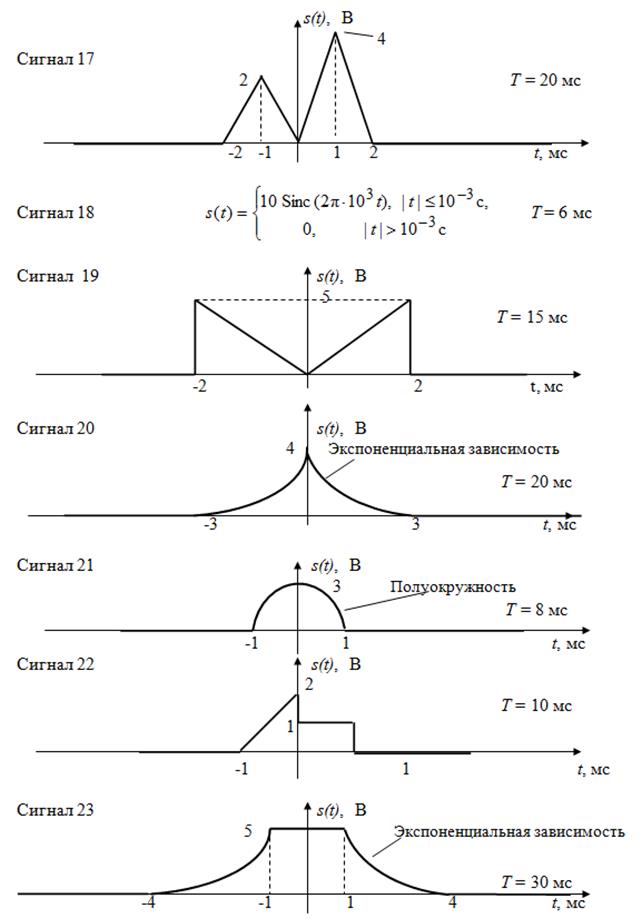
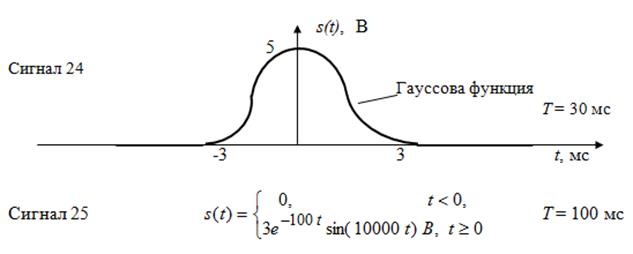
2. РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА № 1 2.1. Содержание задания расчётно-графической работы № 1 Для заданного варианта исследуемого сигнала (сигналы 1 – 25) выполнить следующие задания: 1. Составить математическую модель сигнала s 1 (t) на одном периоде повторения и вычислить его энергию Es. Определить длительность импульсного сигнала t И и его скважность Q. Нарисовать график сигнала на одном периоде повторения. 2. Составить математическую модель периодического сигнала s П (t) указанной формы на всей оси времени и нарисовать график этого сигнала на 3 – 5 периодах повторения. 3. Определить аналитические выражения для амплитудного и фазового спектров периодического сигнала (an, bn, An, fn), построить соответствующие диаграммы. Сделать оценку скорости изменения амплитуды гармоники An в зависимости от её номера n (при n –> ¥). 4. Рассчитать в виде таблицы зависимость энергии сигнала Es(n) от нарастающего количества гармоник при его представлении ограниченным рядом Фурье. Построить график этой зависимости, нормированной к полной энергии сигнала Es на периоде повторения. 5. Определить количество гармоник ограниченного ряда Фурье, сохраняющих не менее 90% (n 90 ) и 99% (n 99 ) энергии исходного сигнала (на одном периоде повторения). Рассчитать и нарисовать формы сигналов для этих случаев. Определить граничную частоту f гр, выше которой имеется 1 и 10% от полной энергии непериодического сигнала. 6. Найти аналитическое выражение спектральной плотности S( w ) непериодического сигнала заданной формы и построить график её модуля. Сопоставить амплитуду n -ой гармоники (см. п. 3, выражение для An) с модулем спектральной плотности | S( w ) |на частоте 7. Получить аналитическое выражение для энергетического спектра W( w ) непериодического сигнала, построить его график. Вычислить эффективную ширину спектра сигнала D f ЭФФ. Вычислить и построить энергетическую характеристику 8. Определить период дискретизации D t исходного сигнала по теореме Котельникова для f гр(10%) и f гр(1%). Записать аналитически, рассчитать и построить график временной зависимости исходного сигнала при его представлении рядом Котельникова для обоих случаев. 9. Двумя способами (непосредственно по сигналу s 1(t) и по энергетическому спектру W( w )) найти аналитическое выражение для функции автокорреляции K Н(t) непериодического сигнала и построить её графически. Вычислить эффективный интервал корреляции сигнала DtЭФ. 10. Определить аналитически и построить графически функцию автокорреляции K П(t)периодического сигнала.
Варианты исследуемых сигналов
Рис. 2.1. Варианты сигналов для выполнения домашнего задания
|

 параметрами сигнала могут быть амплитуда
параметрами сигнала могут быть амплитуда 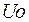 , циклическая частота
, циклическая частота 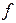 и начальная фаза
и начальная фаза 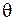 .
. . Определить произведение ширины спектра D f непериодического сигнала на его длительность tИ.
. Определить произведение ширины спектра D f непериодического сигнала на его длительность tИ.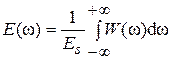 .
.