Автокорреляционная функция непериодического сигнала
АКФ сигнала определяется по формуле
Подставляя в интеграл (2.11) временную функцию сигнала и разбивая его на три части, получим (в формулах t и = T /3 – длительность импульса):
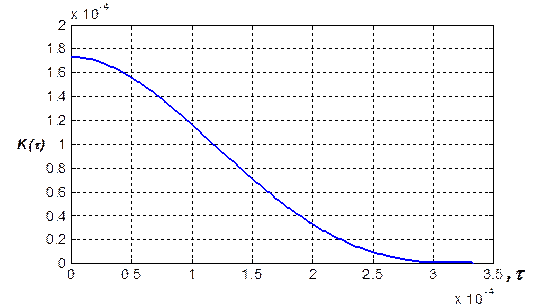
График автокорреляционной функции изображен на рис. 2.10 (ось времени – в мс). Ниже приводится два набора команд системы MATLAB, с помощью которых можно вычислить автокорреляционную функцию непериодического сигнала и построить её график. Первый набор реализует вычисление по формулам, полученным в результате аналитического интегрирования.
Рис. 2.10. Автокорреляционная функция непериодического сигнала при t > 0
tau = linspace(-tu, tu, 512); % Вычисление K(tau) по аналитическим выражениям I1 = Um^2*(tu-abs(tau)).*(cos(W*tau)+... sinc1(W*(tu-abs(tau)))); I2 = Uo*Um*(tu-abs(tau)).*(cos(W*tau/2).*... sinc1(W*(tu-abs(tau))/2); I3 = Uo^2*(tu-abs(tau)); Kt = I1-2*I2+I3; figure(1) plot(tau,Kt)
Второй набор команд вычисляет спектральную плотность сигнала прямым интегрированием по формуле (2.8) методом прямоугольников.
N = 512; % Прямое вычисление K(tau) по сигналу s(t) t = linspace(-tu/2,tu/2,N); dt = t(2)-t(1); s = cosinob1(t,Um,T,Uo); s1 = fliplr(s); K = conv(s,s1)*dt; figure(2) plot(tau,Kt,dt*(-N:N),K)
3. РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА № 2 3.1 Содержание задания расчётно-графической работы № 2 Для своего варианта сигнала (см. сигналы 1 – 25) выполнить следующие задания: 1. Провести масштабирование заданного периодического сигнала s (t), приведя его к масштабу от -1 В до +1 В. Выбрать несущую частоту Примечание. Величина
где 2. Записать математическую модель АМК при модуляции периодическим сигналом и построить графики U АМ(t) при M = 0.8 и M = 1.0 и построить осциллограммы обоих АMК. 3. Построить дискретный спектр АМК с периодической модулирующей функцией при M = 0.8. Вычислить дискретную функцию E АМ(n), n = 0,1,2,…,распределения энергии в спектре АМК. 4. Построить дискретный спектр АМК (M = 0.8) с одной (верхней) боковой полосой (ОБП) и частичным подавлением несущей (U н ОБП = 0.5 U н). Найти распределение энергии в спектре АМК с ОБП. 5. Записать математическую модель сигнала U ОБП(t) с ОБП и построить график этой временной зависимости на двух периодах повторения модулирующего сигнала. 6. Определить аналитически и построить графически временную зависимость углового модулированного колебания при девиации фазы 7. Вычислить с использованием БПФ амплитудную диаграмму 8. Рассчитать и построить временную зависимость частотно-модулированного колебания при девиации частоты, примерно соответствующей индексу фазомодулированного колебания. 9. Вычислить с использованием БПФ спектральную амплитудную диаграмму 10. Определить интервал дискретизации Отчет о выполненном задании должен содержать выводы по результатам сравнения сигналов и особенностей их временных и спектральных характеристик.
|

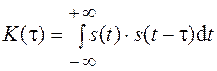 . (2.11)
. (2.11)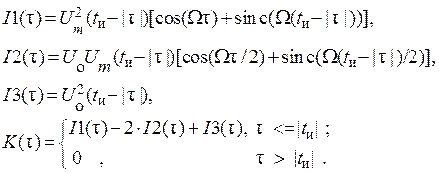
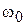 . Принять амплитуду несущей U н = 1 В.
. Принять амплитуду несущей U н = 1 В. определяется из условия
определяется из условия
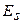 – полная энергия модулирующего сигнала s (t), причём
– полная энергия модулирующего сигнала s (t), причём  ,
, – энергетический спектр этого сигнала.
– энергетический спектр этого сигнала.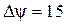 рад.
рад.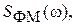 построить её график. Вычислить и построить график
построить её график. Вычислить и построить график 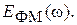 Определить полосу частот, занимаемую ФМК.
Определить полосу частот, занимаемую ФМК.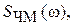 построить её график. Вычислить и построить график
построить её график. Вычислить и построить график  Определить полосу частот ЧМК.
Определить полосу частот ЧМК.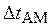 АМК при
АМК при не превышает 5% полной энергии АМК (см. п.3).
не превышает 5% полной энергии АМК (см. п.3).


