Математическая модель АМК
Составляется функция модулирующего сигнала и рассчитывается коэффициент амплитудной модуляции при M = 0.8. Соблюдаются следующие размерности: напряжение – 1 В, время – 1 мс, частота – 1 кГц, круговая частота – 1 крад/с (рис. 3.1).
Uo = 1; Um = 2; T = 1e-3; tau = T/3; W = 2*pi/T; F = 1/T; t = linspace(0,2*T,512); s = cosinobn(t,Um,T,Uo); figure(1) plot(t,s)
Ds = max(s) - min(s); Sam = 2*(s-min(s))/Ds - 1;
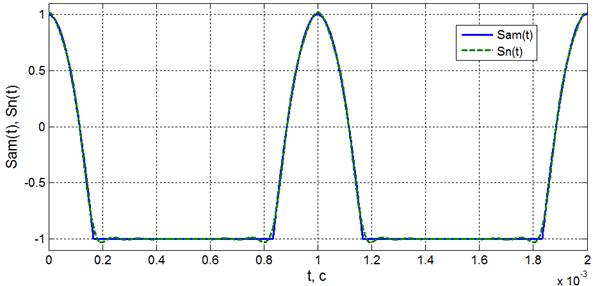
a = [0.2180 0.3910 0.2757 0.1378 0.0276... -0.0276 -0.0315 -0.0098 0.0098 0.0138 0.0050]; as = 2*a/Ds; as(1) = as(1) - (2*min(s) + Ds)/Ds; Sn = as(1); for i=2:length(as); c = as(i)*cos(2*pi*n(i)*t/T); Sn = Sn+c; end figure(2) plot(t,Sam,t,Sn)
Рис. 3.1. Модулирующий сигнал Составляется m- функция АМК, в которой текущее время (переменная t) должно совпадать с подобным текущим временем при определении модулирующего сигнала s (t) в m- функция cosinobn:
function Uam = AMK(t,Un,Fn,s,M) % Uam = AMK(t,Un,Fn,s,M)
Uam = Un*(1+M*s).*cos(2*pi*Fn*t);
Для определения несущей частоты проводится анализ рассчитанных в задании № 1 гармонических составляющих (переменная a) периодического модулирующего колебания. Примем верхнюю частоту модулирующего сигнала s (t) равной частоте той гармоники, амплитуда которой (и всех последующих) меньше 1 % от величины максимальной амплитуды среди гармоник. Здесь по частоте 10-й гармоники (F 10 = 10 кГц) определим частоту несущей, которая должна быть выше от 5 до 10 раз: F n = 5 F 10 = 50 кГц. Зададим амплитуду несущей U n =1 В и построим осциллограмму АМК (рис. 3.2), используя следующие команды системы MATLAB:
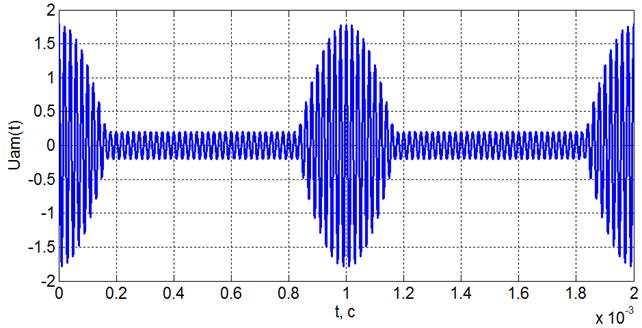
Un = 1; Fn = 50e3; M = 0.8; Uam = AMK(t,Un,Fn,Sam,M) figure (3) plot(t,Uam)
Рис. 3.2. Осциллограмма АМК при M = 0.8 Энергия АМ-сигнала на одном периоде повторения равна
или при обращении к вычислениям в системе MATLAB:
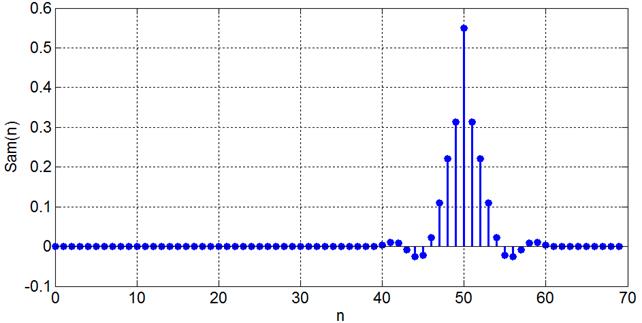
dt = t(2)-t(1); Eam = sum(Uam.^2)*dt/2*1000 3.2.2. Дискретный спектр АМК с периодическим Формирование модели АМК в виде отдельных спектральных составляющих: несущее колебание амплитудой 1 В частотой 50 кГц, что соответствует N = 50 – порядковому номеру гармоники несущего колебания, выраженному через частоту следования модулирующего колебания (1кГц); набор 10 верхних боковых частот Svbn, n = N +(1,…,10); набор 10 нижних боковых частот Snbn, n = N – (1,…,10). Частота несущей равна 50 кГц, боковые составляющие отстоят от неё не более чем на 10 кГц, т.е. полоса частот АМК равна 20 кГц (рис. 3.3).
N = ceil(Fn/F); a1 = as(2:end); Ng = length(a1); Svb = M*Un*[zeros(1,N+1) a1 zeros(1,Ng-1)]/2; Snb = M*Un*[zeros(1,N-Ng) fliplr(a1) zeros(1,2*Ng)]/2; Spam = Svb+Snb; Spam(N+1) = Un*(1+M*as(1)); figure(4) n = 0:N+2*Ng-1; stem(n, Spam)
Рис. 3.3. Амплитудный спектр АМК (M = 0.8) Как следует из рис. 3.4, превышение нормированной энергетической характеристикой уровня 0.95 происходит при учете 53 гармоник частоты следования, то есть частоту FАМ = 53 кГц можно считать верхней частотой спектра исследуемого АМК. Полоса частот 2D f ам, занимаемая АМК, как уже указывалось, составляет 20 кГц.
Eam = cumsum(Spam.^2)/2; % Значение Eam = 0.3111 В2×мс Eam = Eam/max(Eam); n1 = (N-Ng)LN+Ng); figure(5) plot(n1,Eam(n1+1),n1,0.95*ones(1,length(n1)))
|

 , (3.1)
, (3.1)