Частотно-модулированный сигнал

При моделировании на ЭВМ частотно-модулированных колебаний (ЧМК) прямое управление частотой невозможно. Поэтому ЧМК обычно представляется как ФМК, фаза которого вычисляется как интеграл от текущей частоты, изменяющейся по закону модулирующего колебания. Обычно вычисляют интеграл от этого колебания и, умножив на масштабный коэффициент частотной модуляции M_fm, а полную фазу получают как сумму фаз несущей частоты и модулирующего сигнала.

Чтобы определить значение M_fm, соразмерное с выбранным ранее индексом угловой модуляции M_p = 15, определим величину максимального приращения фазы ФМК по команде

dPsi = max(diff(Mp*Umod))/dt;

Эта величина равна 1.6302e+005 рад/с (или 25946 Гц), что означает максимальное отклонение частоты модулированного колебания от частоты несущей, т.е. его девиацию частоты вверх. Поскольку модулирующий сигнал s (t) симметричен относительно вертикальной оси, то и отклонение частоты вниз при фазовой модуляции также симметрично, поэтому максимальная полоса занимаемых ФМК частот около 52 кГц.

При частотной модуляции максимальное приращение фазы также может быть определено по команде

dPsi_fm = max(diff(Mfm*cumsum(Umod)*dt))/dt;

или

dPsi_fm = Mfm*max(Umod);

В нашем случае максимальное значение модулирующего колебания равно 1, поэтому при том же индексе угловой модуляции, что у ФМК, масштабный коэффициент M_fm ЧМК должен быть равен 163020 рад/с. Заметим, что при таком модулирующем колебании (все его значения неотрицательны) девиация вниз отсутствует. Выберем M_fm = 200000:

 

Mfm = 200000;

Psi_fm = 2*pi*Fn*t+Mfm*cumsum(Umod)*dt;

Ufm = Un*cos(Psi_fm);

figure(11)

plot(t,Ufm,t,Umod)

 

Фрагмент временной зависимости ЧМК показан на рис. 3.10, а его амплитудный спектр – на рис. 3.11.

 

Рис. 3.10. Фрагмент осциллограммы частотно-модулированного колебания

Спектральные характеристики ЧМК вычисляются так же, как спектральные характеристики ФМК:

 

Sfm = fft(Ufm)/Nt;

figure(12)

stem(df*(n2-1), 2*abs(Sfm(n2)))

 

Рис. 3.11. Амплитудный спектр частотно-модулированного колебания

Представление временной зависимости на двух периодах модуляции в 4096 точках даёт возможность с помощью БПФ определить спектр ЧМК и его энергетическую характеристику (рис. 3.12).

 

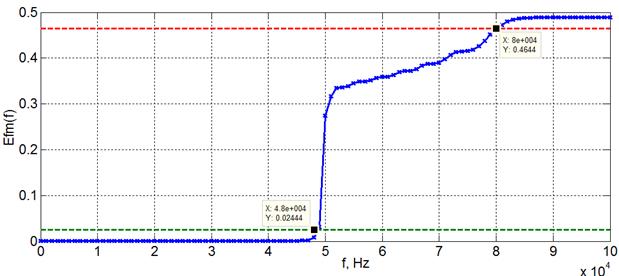
Efm = cumsum(2*abs(Sfm(n2)).^2);

% Граница по уровню 0.05

Gr05=0.05*Efm(end)*ones(1,length(n2));

% Граница по уровню 0.95

Gr95=0.95*Efm(end)*ones(1,length(n2));

figure(13)

plot(df*(n2-1),Efm, df*(n2-1), Gr05, df*(n2-1),Gr95)

 

Рис. 3.12. Энергетическая характеристика ЧМК

Энергетическая характеристика ЧМК находится по формуле

. (3.4)

Полная энергия ЧМК на одном периоде повторения равна

. (3.5)

Верхняя частота спектра ЧМК по уровню 0.95 равна 80 кГц, нижняя частота по уровню 0.05 равна 48 кГц. Ширина спектра частот, определяемая по уровням 5% и 95% от полной энергии ЧМК, равна 2D f _фм = 32 кГц, что в полтора раза больше полосы частот, занимаемой АМК и немного меньше (32 кГц < 39 кГц) полосы частот, занимаемой ФМК.

Заметим, что при выбранном масштабном коэффициенте
M_fm = 200000 девиация частоты вверх равна 200000/(2p) = 31831 Гц.