Преобразование координат
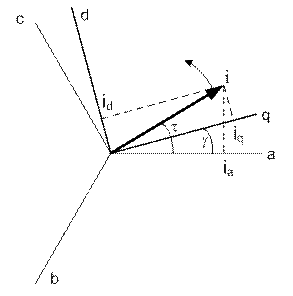
На рис. 1.22 приведена неподвижная система координат a, b, c. Изображающий вектор тока i вращается против часовой стрелки, и его проекции на оси фаз образуют систему фазных токов i a, i b, i c. Положение изображающего вектора определяется углом τ, который отсчитывается от направления оси фазы a. Координатная система d-q вращается в том же направлении. Её положение определяется углом γ. Проекции изображающего вектора тока I на оси d-q образуют систему токов в продольной i d и поперечной i q осях. Очевидно, что i q = i cos(τ – γ); i d = i sin(τ – γ). Соотношение между фазным током i a и токами в продольной i d и поперечной i q осях можно записать в виде (рис. 1.22) i a = i q cosγ – i d sinγ. Аналогично для токов i b и i c i b = i q cos(γ – ρ) – i d sin(γ – ρ); i c = i q cos(γ + ρ) – i d sin(γ + ρ), где ρ = 2π/3.
Рис. 1.22. Преобразование координат
Обратные соотношения, т. е. соотношения между токами в продольной i d и поперечной i q осях и фазными токами i a, i b, i c, имеют вид
|