1. Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О 1 есть геометрическое место всех точек пространства, находящихся от точки О 1 на расстоянии R. 2. Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в её плоскости, называется поверхностью вращения. Пусть некоторая прямая L лежит в плоскости Oyz. Уравнения этой кривой запишутся в виде 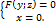 Возьмём на поверхности произвольную точку М(x;y;z). Проведём через т. М плоскость, перпендикулярную оси Оz, и обозначим точки пересечения с осью Оz и кривой L соответственно через О 1 и N. Обозначим координаты точки N(0;y1;z1). Отрезки О1М и О1N являются радиусами одной и той же окружности. Поэтому О1М=О1N. Но О1М=
Возьмём на поверхности произвольную точку М(x;y;z). Проведём через т. М плоскость, перпендикулярную оси Оz, и обозначим точки пересечения с осью Оz и кривой L соответственно через О 1 и N. Обозначим координаты точки N(0;y1;z1). Отрезки О1М и О1N являются радиусами одной и той же окружности. Поэтому О1М=О1N. Но О1М=  , О1N=
, О1N= 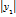 . Следовательно,
. Следовательно, 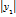 =
=  или у1 = ±
или у1 = ±  . Кроме того
. Кроме того  . F(±
. F(±  ;z)=0 - yравнение поверхности вращения, ему удовлетворяют координаты любой точки М этой поверхности и не удовлетворяют координаты точек, не лежащих на поверхности вращения. 3. Поверхность образованная прямыми линиями, проходящими через данную точку Р и пересекающими данную плоскую линию L (не проходящую через Р), называется конической поверхностью или конусом. При этом линия L называется направляющей конуса, точка Р- её вершиной, а прямая, описывающая поверхность, называется образующей.Пусть направляющая L задана уравнениями
;z)=0 - yравнение поверхности вращения, ему удовлетворяют координаты любой точки М этой поверхности и не удовлетворяют координаты точек, не лежащих на поверхности вращения. 3. Поверхность образованная прямыми линиями, проходящими через данную точку Р и пересекающими данную плоскую линию L (не проходящую через Р), называется конической поверхностью или конусом. При этом линия L называется направляющей конуса, точка Р- её вершиной, а прямая, описывающая поверхность, называется образующей.Пусть направляющая L задана уравнениями 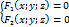 , а точка Р (
, а точка Р ( )- вершина конусаВозьмём на поверхности конуса произвольную точку М
)- вершина конусаВозьмём на поверхности конуса произвольную точку М  . Образующая, проходящая через т. М и Р, пересечёт направляющую L в некоторой точке N(х1;y1;z1). Координаты т. N удовлетворяют уравнениям направляющей:
. Образующая, проходящая через т. М и Р, пересечёт направляющую L в некоторой точке N(х1;y1;z1). Координаты т. N удовлетворяют уравнениям направляющей: 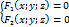 . Канонические уравнения образующих, проходящих через точки Р и N имеют вид
. Канонические уравнения образующих, проходящих через точки Р и N имеют вид 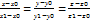 . 4. Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую К, называется цилиндрической поверхностью или цилиндром. При этом кривая К называется направляющей цилиндра, а прямая L его образующей. Пусть в плоскости Оху лежит некоторая линия К, уравнение которой F(x;y)=0. Построим цилиндр с образующими параллельными оси Оz и направляющей К. Возьмём на цилиндре любую т. М
. 4. Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую К, называется цилиндрической поверхностью или цилиндром. При этом кривая К называется направляющей цилиндра, а прямая L его образующей. Пусть в плоскости Оху лежит некоторая линия К, уравнение которой F(x;y)=0. Построим цилиндр с образующими параллельными оси Оz и направляющей К. Возьмём на цилиндре любую т. М  . Она лежит на какой-то образующей. Пусть N- точка пересечения этой образующей с плоскостью Оху. Следовательно,т.N лежит на кривой К и её координаты удовлетворяют уравнению F(x;y)=0. Этому уравнению удовлетворяют координаты т. М
. Она лежит на какой-то образующей. Пусть N- точка пересечения этой образующей с плоскостью Оху. Следовательно,т.N лежит на кривой К и её координаты удовлетворяют уравнению F(x;y)=0. Этому уравнению удовлетворяют координаты т. М  .И так как М- любая точка цилиндра, то F(x;y)=0 и будет уравнением цилиндра.
.И так как М- любая точка цилиндра, то F(x;y)=0 и будет уравнением цилиндра.

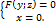 Возьмём на поверхности произвольную точку М(x;y;z). Проведём через т. М плоскость, перпендикулярную оси Оz, и обозначим точки пересечения с осью Оz и кривой L соответственно через О 1 и N. Обозначим координаты точки N(0;y1;z1). Отрезки О1М и О1N являются радиусами одной и той же окружности. Поэтому О1М=О1N. Но О1М=
Возьмём на поверхности произвольную точку М(x;y;z). Проведём через т. М плоскость, перпендикулярную оси Оz, и обозначим точки пересечения с осью Оz и кривой L соответственно через О 1 и N. Обозначим координаты точки N(0;y1;z1). Отрезки О1М и О1N являются радиусами одной и той же окружности. Поэтому О1М=О1N. Но О1М=  , О1N=
, О1N= 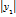 . Следовательно,
. Следовательно,  . F(±
. F(± 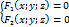 , а точка Р (
, а точка Р ( )- вершина конусаВозьмём на поверхности конуса произвольную точку М
)- вершина конусаВозьмём на поверхности конуса произвольную точку М  . Образующая, проходящая через т. М и Р, пересечёт направляющую L в некоторой точке N(х1;y1;z1). Координаты т. N удовлетворяют уравнениям направляющей:
. Образующая, проходящая через т. М и Р, пересечёт направляющую L в некоторой точке N(х1;y1;z1). Координаты т. N удовлетворяют уравнениям направляющей: 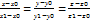 . 4. Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую К, называется цилиндрической поверхностью или цилиндром. При этом кривая К называется направляющей цилиндра, а прямая L его образующей. Пусть в плоскости Оху лежит некоторая линия К, уравнение которой F(x;y)=0. Построим цилиндр с образующими параллельными оси Оz и направляющей К. Возьмём на цилиндре любую т. М
. 4. Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую К, называется цилиндрической поверхностью или цилиндром. При этом кривая К называется направляющей цилиндра, а прямая L его образующей. Пусть в плоскости Оху лежит некоторая линия К, уравнение которой F(x;y)=0. Построим цилиндр с образующими параллельными оси Оz и направляющей К. Возьмём на цилиндре любую т. М 


