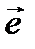Пусть функция  определена в некоторой окрестности точки М (х;у). Приращение функции в точке М:
определена в некоторой окрестности точки М (х;у). Приращение функции в точке М:
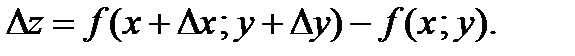 Функция
Функция  называется дифференцируемой в точке М (х;у), если ее полное приращение в этой точке можно представить в виде:
называется дифференцируемой в точке М (х;у), если ее полное приращение в этой точке можно представить в виде:
 ,где
,где 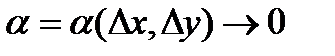 и
и  при
при 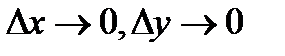 . Сумма первых двух слагаемых представляет собой главную часть приращения функции.Главная часть приращения функции
. Сумма первых двух слагаемых представляет собой главную часть приращения функции.Главная часть приращения функции  , линейная относительно
, линейная относительно 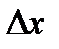 и
и 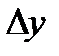 , называется полным дифференциалом этой функции и обозначается символом dz:
, называется полным дифференциалом этой функции и обозначается символом dz: 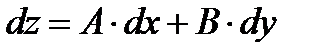
80. Производная по направлению. Градиент.
Градие́нт — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении. С математической точки зрения градиент — это производная скалярной функции, определенной на векторном пространстве.Обозначается: 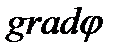 .Рассмотрим функцию
.Рассмотрим функцию 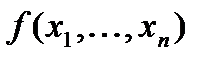 от n аргументов в окрестности точки
от n аргументов в окрестности точки  . Для любого единичного вектора
. Для любого единичного вектора 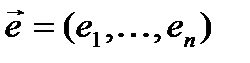 определим производную функции f в точке
определим производную функции f в точке 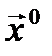 по направлению
по направлению  следующим образом:
следующим образом: 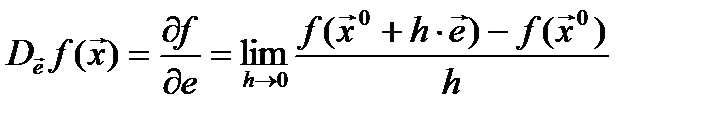 Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора 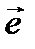 .
.
Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
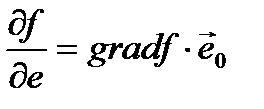 ,где
,где 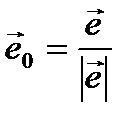 — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора
— орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора 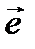

 определена в некоторой окрестности точки М (х;у). Приращение функции в точке М:
определена в некоторой окрестности точки М (х;у). Приращение функции в точке М: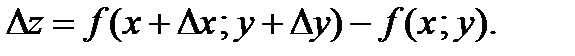 Функция
Функция  называется дифференцируемой в точке М (х;у), если ее полное приращение в этой точке можно представить в виде:
называется дифференцируемой в точке М (х;у), если ее полное приращение в этой точке можно представить в виде: ,где
,где 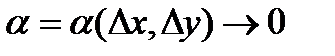 и
и  при
при 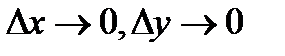 . Сумма первых двух слагаемых представляет собой главную часть приращения функции.Главная часть приращения функции
. Сумма первых двух слагаемых представляет собой главную часть приращения функции.Главная часть приращения функции 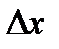 и
и 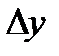 , называется полным дифференциалом этой функции и обозначается символом dz:
, называется полным дифференциалом этой функции и обозначается символом dz: 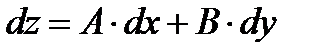
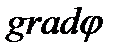 .Рассмотрим функцию
.Рассмотрим функцию 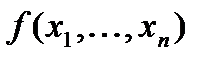 от n аргументов в окрестности точки
от n аргументов в окрестности точки  . Для любого единичного вектора
. Для любого единичного вектора 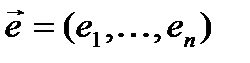 определим производную функции f в точке
определим производную функции f в точке 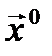 по направлению
по направлению  следующим образом:
следующим образом: 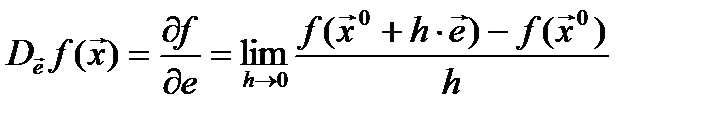 Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора 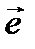 .
.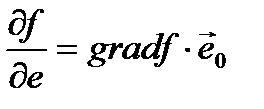 ,где
,где 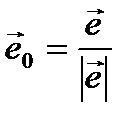 — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора
— орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора