Поверхности уровня. Уравнение касательной плоскости к поверхности.
Поверхность уровня функции u=f(х, у, z) или поверхность уровня скалярного поля — поверхность, задаваемая уравнением f (х, у, z)=С, где С — постоянная. В точках поверхности уровня функция принимает заданное постоянное значение u = С. Пусть М – точка поверхности S. Плоскость, содержащая точку М и обладающая тем свойством, что расстояние от этой плоскости до переменной точки M1 поверхности S является бесконечно малым по сравнению с расстоянием ММ1, называется касательной плоскостью к поверхности S в точке М. Если поверхность в трехмерном пространстве задана уравнением f(x; y; z) = 0, где функция f достаточное число раз дифференцируема, то уравнение плоскости, касательной к этой поверхности в точке
Если же поверхность задана уравнением, разрешенным относительно аппликаты z, т.е. имеет вид z = z(x; y), то уравнение касательной плоскости принимает вид:
|
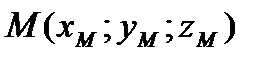, имеет вид:
, где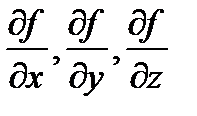 
– частные производные функции трех переменных f(x; y; z) по этим переменным.
