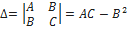Экстремумы функций двух переменных.
Пусть функция z = f(x; y) определена в некоторой области D, точка N(x 0 ;y 0 ) є D. Условия экстремума. Если в точке N(x 0; y 0) дифференцируемая функция z = f(x; y) имеет экстремум, то ее частные производные в этой точке равны нулю: f’(x 0;y 0) =0, f’(x 0;y 0) = 0. Точка, в которой частные производные первого порядка функции z = f(x; y) равны нулю, т. е. f’x= 0, f’y= 0, называется стационарной точкой функции z. Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими. В критических точках функция может иметь экстремум, а может и не иметь. Пусть в стационарной точке (x 0;y 0) и некоторой ее окрестности функция f(x;y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (х 0; y 0) значения А= f”xx(x 0; у 0), В == f”xy(x 0; у 0), С = f”yy(x 0; y 0). Обозначим
Тогда: 1) если ∆ >0, то функция f(x; y) в точке (х 0; y 0) имеет экстремум: максимум, если А<0; минимум, если А >0; 2) если ∆ <0, то функция f(x; y) в точке (x 0;y 0) экстремума не имеет. 3)В случае ∆ = 0 экстремум в точке (х 0;у 0) может быть, может не быть. Необходимы дополнительные исследования.
|