Разработать усиление стальной балки при заданном увеличении нагрузки устройством двухстоечного шпренгеля.
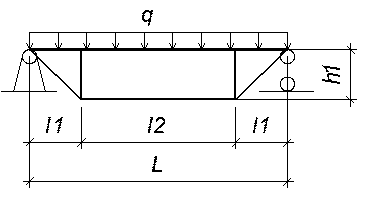
Высота шпренгеля h1=L/5=1 м. Принимаю размеры: l1=h1=1м; l2=L-2l1=4м.
Рис. 11. Схема балки, усиленной шпренгелем.
Рассматриваю балку как неразрезную статически неопределимую систему, нагруженную нагрузкой q=128,3 кН/м. Определяю действующие в системе усилия методом сил. Строю основную систему.
Рис. 12. Основная система.
Неизвестную реакцию в дополнительной опоре нахожу с помощью метода сил. Основное уравнение:
Строю эпюру моментов от единичного загружения (X1=1, P=0). Опорные реакции будут равны:
Т.к. эпюра симметрична относительно середины пролета, достаточно найти координаты левой ее части:
Рис. 13. Эпюра моментов единичного загружения.
Строю эпюру моментов от грузового загружения (X1=0, P≠0). Опорные реакции будут равны:
Координаты эпюры грузового загружения:
Рис. 14. Грузовая эпюра моментов.
Нахожу коэффициенты уравнения метода сил:
Решаю уравнение метода сил и нахожу неизвестную реакцию в дополнительной опоре:
Строю эпюру моментов МХ, координаты которой нахожу по формуле:
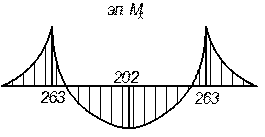
Рис. 15. Итоговая эпюра моментов.
|
.
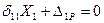-1.
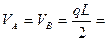384,9 кН.
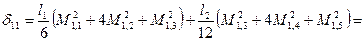10,06.
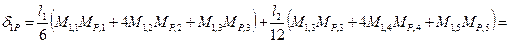-4627,6.
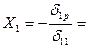460 кН.
.
139 кНм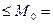 
444 кНм.
