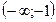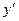Решение. При исследовании функции методами дифференциального исчисления необходимо:
При исследовании функции методами дифференциального исчисления необходимо: а) найти область определения функции; б) исследовать функцию на непрерывность; в) найти точки пересеченияи графика функции с осями координат; г) определить интервалы возрастания и убывания функции и точки ее экстремума; д) найти интервалы выпуклости, и вогнутости функции и точки перегиба графика функции.
а) Областью определения данной функции является множество всех действительных чисел. б) Данная функция является элементарной,.поэтому она непрерывна -в на своей области определения, то есть на интервале в) Для нахождения точки пересечения графика функции с осью Оу подставим -в уравнение функции х x= 0. Тогда у = 5. Значит, график функции пересечет ось Оу в точке А(0; 5). Для определения точки пересечения исследуемой кривой с осью Ох следует решить уравнение
г) Для (нахождения интервалов возрастания и убывания функции определим интервалы знакопостоянства ее первой производной.
y1 = x2 – 2x – 3
Корнями производной являются х1 = — 1, х2 = 3 (критические точки первого рода). Промежутки знакопостоянства производной у' определяем, как и в предыдущей задаче, методом интервалов. (рис. 5).
       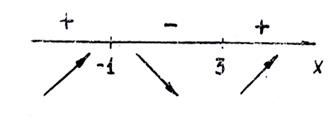 + _ + Рис.5 + _ + Рис.5
Данная функции возрастает на интервалах
Для исследования критических точек х1 =— 1 и х2 = 3 на экстремум воспользуемся первым достаточным признаком экстремума функции: если функция f(х) дифференцируема в точке
При переходе через точку х1 = — 1 Ymax = y(-1) = 6 2/3 ЗЗначит, Так как при переходе через точку х2= 3 то С(3; -—4) - —точка минимума.
д) Для определения интервалов выпуклости и вогнутости и точек перегиба графика функции используем следующие достаточные признаки: если вторая производная если Найдем вторую производную данной функции:
На интервале На интервале Так как при переходе через точку х=1 вторая производная меняет свой знак, то х=1 есть абсцисса точки перегиба.
Результаты исследований приведены в таблице 3.
График функции изображен на рис. 2.
рис. 2 Вопросы для самопроверки
1. Сформулируйте теоремы Ролля, Лагранжа. Каков их геометрический смысл? 2. Какая функция называется возрастающей? убывающей? 3. Сформулируйте достаточные признаки возрастания и убывания функции. 4. Какие точки называют критическими точками функции? 5. Назовите достаточные признаки экстремума функции. 6. Какая кривая называется выпуклой? (вогнутой?) 7. Как найти интервалы выпуклости и вогнутости кривой? 8. Что называется точкой перегиба кривой? 9. Сформулируйте достаточный признак существования точки перегиба кривой. 10. Назовите схему исследования функции и построения ее графика.
|


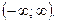 (—;).
(—;).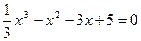 1/3 x3-x2 – 3x+5 = 0. Из-за отсутствия целочисленных корней этого уравнения его решение громоздко (оно может быть найдено, например, по формулам Кардано) и не приводится здесь.
1/3 x3-x2 – 3x+5 = 0. Из-за отсутствия целочисленных корней этого уравнения его решение громоздко (оно может быть найдено, например, по формулам Кардано) и не приводится здесь.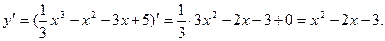
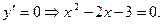
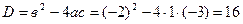

 - точки, подозрительные на экстремум.
- точки, подозрительные на экстремум.
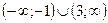 (—; —1) и (3; ) (здесь производная у' положительна) и убывает на интервале (—-1; 3) (здесь у'<0).
(—; —1) и (3; ) (здесь производная у' положительна) и убывает на интервале (—-1; 3) (здесь у'<0).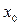 и ее окрестности и ее производная
и ее окрестности и ее производная  слева от этой точки положительна (отрицательна), а справа — отрицательна (положительна), то в точке
слева от этой точки положительна (отрицательна), а справа — отрицательна (положительна), то в точке 
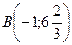 В (-1; 6 2/3) – точка максимума.
В (-1; 6 2/3) – точка максимума.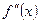 дважды дифференцируемой функции f(х) положительна (отрицательна) в каждой точке интервала (а; b), то на этом интервале график функции f(x) является вогнутым (выпуклым);
дважды дифференцируемой функции f(х) положительна (отрицательна) в каждой точке интервала (а; b), то на этом интервале график функции f(x) является вогнутым (выпуклым); x0 (а; Ь) и
x0 (а; Ь) и  либо
либо 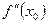 не существует и при /переходе через точку
не существует и при /переходе через точку  - точка перегиба кривой у = f(х).
- точка перегиба кривой у = f(х).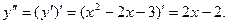
 – точка, подозрительная на перегиб.
– точка, подозрительная на перегиб.
 - +
- +
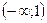 вторая производная отрицательна, поэтому график функции на этом интервале является выпуклой кривой;
вторая производная отрицательна, поэтому график функции на этом интервале является выпуклой кривой;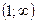 вторая производная положительна, поэтому график функции вогнут на этом интервале.
вторая производная положительна, поэтому график функции вогнут на этом интервале.
 - точка перегиба кривой.
- точка перегиба кривой.