Тема 2. Определители и системы линейных уравнений
Литература: [3] гл.XVII §1-6, [5], № 408,412,471
Определителем второго порядка
Определителем третьего порядка
Минором элемента определителя третьего порядка называется определитель второго порядка, получающийся из данного определителя вычеркиванием строки и столбца, на пересечении которых расположен рассматриваемый элемент.
Алгебраические дополнением элемента определителя называется минор этого элемента, взятый со своим знаком, если сумма номеров строки и столбца, определяющих этот элемент, есть число четное, и с противоположным знаком, если это число нечетное.
Так, например, разложение определителя третьего порядка по элементам третьей строки имеет следующий вид:
Рассмотрим способ решения системы трех линейных уравнений с тремя неизвестными x, y, z с помощью определителей.
Введем обозначение
из определителя
Если определитель
Если то система имеет бесчисленное множество решений.
Задача 24. Решить систему уравнений:
Решение. Вычислим определитель
Так как Вычисляем определители
Вопросы для самопроверки
1. Что называется определителем второго и третьего порядка? 2. Что называется минором элемента определителя? 3. Что называется алгебраическим дополнением элемента определителя? 4. Назовите свойства определителей. 5. При каком условии система трех линейных уравнений с тремя неизвестными имеет единственное решение? Как найти это решение? 6. При каких условиях система уравнений не имеет решений, имеет бесчисленное множество решений?
|

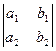 называется число, которое вычисляется по формуле a1b2 – a2b1.
называется число, которое вычисляется по формуле a1b2 – a2b1. называется число, которое вычисляется по формуле a1b2c3 + a2b3c1 + a3b1c2 – a1b3c2 – a2b1c3 – a3b2c1.
называется число, которое вычисляется по формуле a1b2c3 + a2b3c1 + a3b1c2 – a1b3c2 – a2b1c3 – a3b2c1.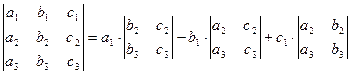
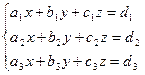
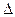 - определитель системы, составленный из коэффициентов при неизвестных.
- определитель системы, составленный из коэффициентов при неизвестных.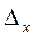 ,
,  ,
,  - вспомогательные определители, получаемые
- вспомогательные определители, получаемые ,
, 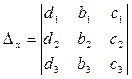 ,
, 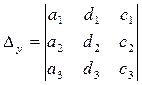 ,
, 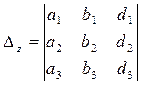
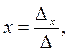 ,
, 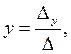 ,
,  .
.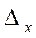 ,
,  ,
,

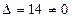 , данная система имеет единственное решение.
, данная система имеет единственное решение.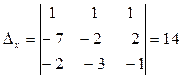 ,
, 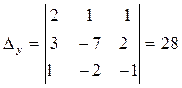 ,
, 
 ,
,  ,
, 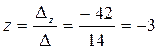 .
.


