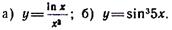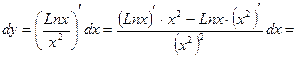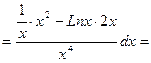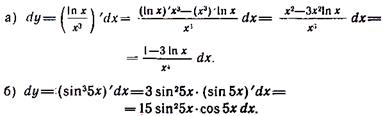Тема 3. Введение в анализ
Литература: [3], гл. VI, § 1—9, упр. 2, 3, 9, гл. VII, § 1—13, упр. 1, 5--10, гл. VIII, § 1-6, упр. 1, 5, 8.
Разберите решение задачи 5. Задача 35. Вычислить пределы:
а) в) д)
Решение.
а) При вычислении пределов удобно пользоваться следующим правилом: если функция у = f(xх) непрерывна при xx = а, то Х-+- I Под знаком предела имеем элементарную функцию, непрерывную при x х = 3. Поэтому для вычисления предела достаточно вместо xх подставить егою предельное значение:
в) ППодстановка предельного значения аргумента xх =2 приводит к неопределенному выражению вида
г) При х->
г) Подстановка предельного значения аргумента приводит к неопределенному выражению вида Для устранения этой неопределенности разделим числитель и знаменатель дроби на х2 (наивысшую степень стоящих в числителе и знаменателе дроби многочленов) и применим основные теоремы о пределах:
д) Подстановка предельного значения аргумента в выражение
(
Для устранения получившейся здесь неопределенности вида — разделим числитель, и знаменатель последней дроби на х.
Эта формула называется формулой первымого замечательнымого пределома. Из нее вытекает следующее следствие:
где k — отличное от нуля число.
ж) Для решения воспользуемся вторым замечательным пределом, который имеет две формы записи:
Вопросы для самопроверки
1. Какие величины -называются постоянными? переменными? 2. Сформулируйте определение функции. 3. Что называется областью определения функции? областью изменения функции? 4. Назовите способы задания функциональной зависимости. 5. Перечислите основные элементарные функции. 6. Что называется числовой последовательностью? 7. Что называется пределом числовой последовательности? 8. Что называется пределом функции? 9. Сформулируйте основные теоремы о пределах функций. 10. Какие величины называются бесконечно малыми? бесконечно большими? 11. Перечислите свойства бесконечно малых и бесконечно больших величин. 12. Напишите формулы первого и второго замечательных пределов. 13. Сформулируйте понятия односторонних пределов функции в точке. 14. Какая функция называется непрерывной в точке? (на отрезке?) 15. Приведите классификацию точек разрыва функции. 16. Назовите свойства непрерывных на отрезке функций.
Тема 4. Производная и дифференциал функции Литература [3]|, гл. IX, § 1—5, гл. X, § 1- — 15, упр. 1—-20, гл. XII, § 1—-7, упр. 1—-5, 7. Для справок приведем основные правила и формулы дифференцирования элементарных и сложных функций.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21.
23.
Разберите решение задач 6, 7. Задача 46. Найти производные данных функций: а) в) д)
Решение. а) Преобразуем давшую ффункцию к следующему виду:
Применив правило (31) дифференцирования суммы функций и формулы (15), (6),(94), получим:
в) Для нахождения производной функции используем правило (53) дифференцирования частного, формулы (31), (1610), (1711), (14), (8). Заметим, что
Эта функция — сложная; запишем ее в виде у= — ½ ln u
u = 3x4 +2.По правилуу (148) дифференцирования сложной функции имеем:
Задача 57. Найти дифференциалы - следующих функций: а)
Решение. Дифференциал dyу функции у = f(х) /равен произведению производной у' на дифференциал dxх аргумента х, то есть dyy = yу'dxх. а)
б)
Вопросы для самопроверки
1. Что называется производной функции? 2. Каков геометрический смысл производной? (ее физический смысл?) 3. Напишите правила и формулы дифференцирования основных элементарных функций. 4. Как найти производную сложной функции? 5. Что называется дифференциалом функции? 6. Каков геометрический смысл дифференциала функции? 7. Перечислите свойства дифференциала функции.
|

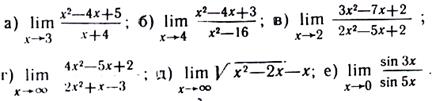
 б)
б) 
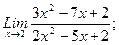 г)
г) 
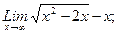 е)
е) 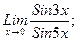 ж)
ж) 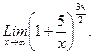
 lim f(х)=f(а).
lim f(х)=f(а).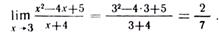
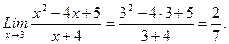
 б) При x х = 4 числитель д(Дроби равен 3, а ее знаменатель равен нулю., т.е. пПри x=4х 4 числитель является ограниченной функцией, а знаменатель есть функция бесконечно малая. Поэтому дробь является бесконечно большой. и ее П(Пределредел бесконечно большой функции обозначают символом (
б) При x х = 4 числитель д(Дроби равен 3, а ее знаменатель равен нулю., т.е. пПри x=4х 4 числитель является ограниченной функцией, а знаменатель есть функция бесконечно малая. Поэтому дробь является бесконечно большой. и ее П(Пределредел бесконечно большой функции обозначают символом ( (ббесконечность), то есть
(ббесконечность), то есть 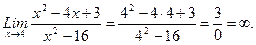

 0/0. Для устранения этой неопределенности разложим числитель и знаменатель дроби на линтейные множители по формуле
0/0. Для устранения этой неопределенности разложим числитель и знаменатель дроби на линтейные множители по формуле 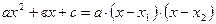 , где
, где  - корни уравнения
- корни уравнения 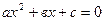 и сократим дробь на (xх—2).). Такое сокращение здесь возможно, так как множитель (х—2) отличен от нуля три х->2:
и сократим дробь на (xх—2).). Такое сокращение здесь возможно, так как множитель (х—2) отличен от нуля три х->2: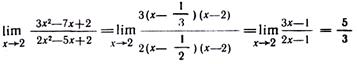
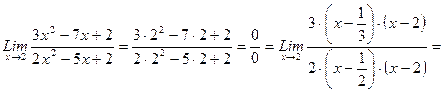

 . Для устранения этой имеем неопределенное выражение вида неопределенности
. Для устранения этой имеем неопределенное выражение вида неопределенности
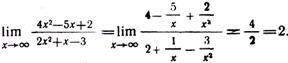
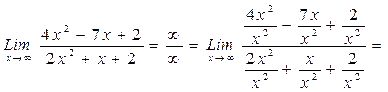
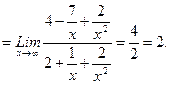
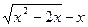 приводит к неопределенному выражению вида
приводит к неопределенному выражению вида  . Для устранения этой неопределенности
. Для устранения этой неопределенности д) При х-> выражение х2—2х—х дает неопределенность.вида —. Для ее устранения умножим и.разделим это выражение на сопряженное выражение, т.е. выражение с противоположным знаком.
д) При х-> выражение х2—2х—х дает неопределенность.вида —. Для ее устранения умножим и.разделим это выражение на сопряженное выражение, т.е. выражение с противоположным знаком.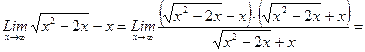 (х2—2х+х):
(х2—2х+х):
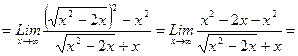
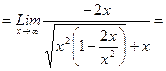

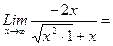
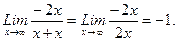
 при
при 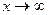 )
) е) Известно, что предел отношения синуса бесконечно малой дуги к самой дуге равен единице, то есть
е) Известно, что предел отношения синуса бесконечно малой дуги к самой дуге равен единице, то есть 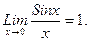

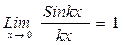 ,
, Преобразуем стоящее под знаком предела выражение, воспользуемся свойствами (пределов и следствием из формулы первого замечательного предела. Тогда
Преобразуем стоящее под знаком предела выражение, воспользуемся свойствами (пределов и следствием из формулы первого замечательного предела. Тогда 
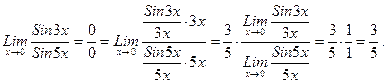
 или
или 

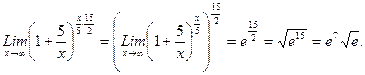


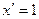
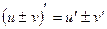
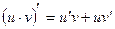
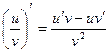

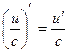
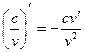
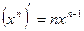 9.
9. 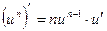
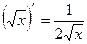 10.
10. 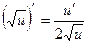
 11.
11. 
 12.
12. 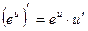
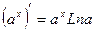 13.
13. 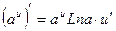
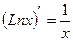 14.
14. 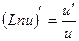
 15.
15. 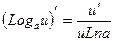
 16.
16. 
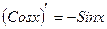 17.
17. 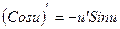
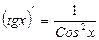 18.
18. 
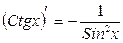 19.
19. 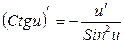
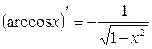 20.
20. 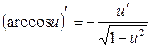
 21.
21. 
 22.
22.  22.
22. 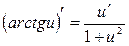
 23.
23. 

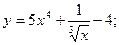 б)
б) 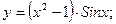
 г)
г) 
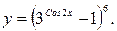


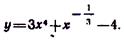
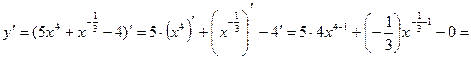
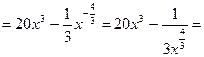
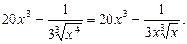
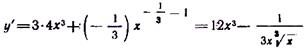
 6) Применим.правило (42) дифференцирования произведения функций и формулы (31), (95), (1610).
6) Применим.правило (42) дифференцирования произведения функций и формулы (31), (95), (1610).

 - сложные тригонометрические функции вида
- сложные тригонометрические функции вида 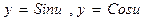 где
где 

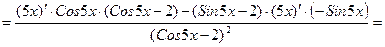

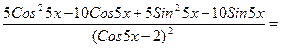

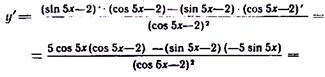
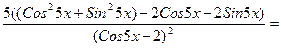
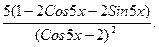

 г) Преобразуем данную функцию, используя свойство логарифма корня:
г) Преобразуем данную функцию, используя свойство логарифма корня: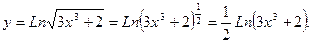
 , где
, где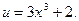
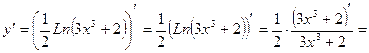
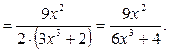
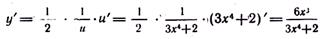
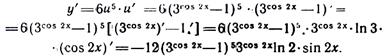 д) Данная функция является сложной. Обозначим 3cos 2x – 1 = u.
д) Данная функция является сложной. Обозначим 3cos 2x – 1 = u.  Тогдатогда у = u6. По правилу (9) и (13) дифференцирования сложной функции имеем:Используя (18), имеем
Тогдатогда у = u6. По правилу (9) и (13) дифференцирования сложной функции имеем:Используя (18), имеем




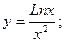 б)
б)