Тема 5. Приложения производной
Литература: [(3], гл. XI, § 1—-3, 7-10; [5], гл.7, §4.\Ь 1162, 1167, 1201. Разберите решение задач 8—11. Задача 8. Напишите уравнения касательной и нормали к кривой у = х2 +1 в точке с абсциссой х0= 2. Решение. Уравнение касательной к кривой у=f(х) в точке M0 (x0; y0) имеет вид y – y0= y (x0)(x-x0) (1)
Определим ординату y0 точки касания: y0 = 22 +1 =2 Найдем значение производной функции в точке касания: y1 = 2x; y1(x0) = 4 По формуле (1) находим уравнение касательной: y-5 = 4(x-2); 4x-y-3=0 Используя формулу (2) находим уравнение нормали: y-5= -1/4(x-2); x+4y-22=0 Задача 9. Найти интервалы -возрастания и убывания функции у = х3—6х2 +9х—1. Решение Функция у = f(х) называется возрастающей (убывающей) на интервале (а; Ь), если для любых значений x1 и х2 аргумента х таких, что а<х1<х2<Ь, выполняется неравенство f(Х2)>f(Х1) (f(x2)f(x1)). Для 'нахождения интервалов возрастания и убывания функции -воспользуемся следующими достаточными признаками: если производная дифференцируемой функции положительна (отрицательна) на некотором интервале, то функция возрастает (убывает) на этом интервале.
Определим промежутки знакопосгоянства производной у', используя метод интервалов. На числовой оси отметим в порядке возрастания критические значения x1=1 и x2 = 3 аргумента x (в этих точках производная данной функция обращается в нуль) (рис. 4). Эти точки разбивают числовую ось на три интервала: (—; 1), (1; 3), (3; ).
В первом и третьем интервалах производная у' положительна, следовательно, функция у здесь возрастает; на втором интервале у' отрицательна и данная функция убывает. Задача 6 10. Исследовать функцию
|

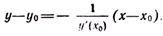 Нормаль (прямая, проходящая через точку касания перпендикулярно касательной) определяется уравнением
Нормаль (прямая, проходящая через точку касания перпендикулярно касательной) определяется уравнением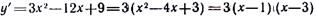 Продифференцируем данную функцию:
Продифференцируем данную функцию: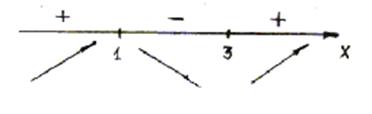 Рис.4
Рис.4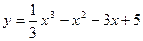 у= 1/3x3-x2-3x+5 и построить ее график.
у= 1/3x3-x2-3x+5 и построить ее график.


