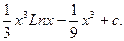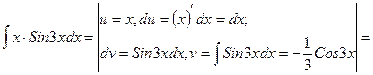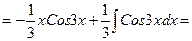Свойства неопределенного интеграла
1. Неопределенный интеграл от суммы конечного числа непрерывных функций равен сумме неопределенных интегралов от слагаемых функций, то есть 2. Отличный от нуля постоянный множитель можно выносить за знак неопределенного интеграла, то есть
3. Дифференциал неопределенного интеграла равен подынтегральному выражению, то есть 4. Неопределенный интеграл от дифференциала функции равен самой функции, сложенной с произвольной постоянной, то есть
Таблица основных интегралов
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13.
Задача 7. Вычислить неопределенные интегралы: а) в) Решение.
а) Преобразуем подынтегральную функцию, применим свойства (1) и (2) неопределенного интеграла и формулы (1) и (4).
б) Рассматриваемый интеграл (как и последующие) вычислим методом замены переменной (методом подстановки), описываемый следующей формулой:
После вычисления неопределенного интеграла, стоящего в правой части формулы (*), в полученном выражении следует перейти от переменной t к переменной х.
в) Данный интеграл сводится к табличному (2), подстановкой l-x3 = t.
г)
д)
Задача 8. Вычислить неопределенные интегралы: а)
Решение.
Данные интегралы вычисляются по формуле интегрирования по частям:
Представление подынтегрального выражения в виде множителей u и dv сводит к интегралу, который должен быть «проще» исходного или табличным интегралом. При этом удобно пользоваться следующими рекомендациями.
1. Если подынтегральная функция содержит произведение многочлена на показательную или тригонометрическую функцию, то за множитель u следует принять многочлен.
2. Если подынтегральная функция содержит произведение многочлена на логарифмическую или обратную тригонометрическую функцию, то за множитель u следует принять логарифмическую или обратную тригонометрическую функцию.
а) Исходя из рекомендации 1, получим
Замечание: интеграл
б) Исходя из рекомендации 2, получим
в) Исходя из рекомендации 1, получим
Вопросы для самопроверки
1. Какая функция называется первообразной для данной функции? 2. Что называется неопределенным интегралом от данной функции? 3. Назовите свойства неопределенного интеграла. 4. Напишите табличные формулы неопределенных интегралов. 5. В чем сущность метода подстановки в неопределенном интеграле? 6. Напишите формулу интегрирования по частям для неопределенного интеграла.
|





 где
где 
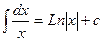

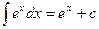
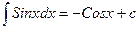


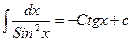

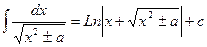
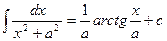
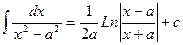

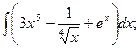 б)
б) 
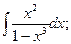 г)
г)  д)
д) 
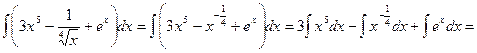


 (*)
(*)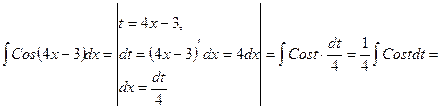
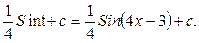
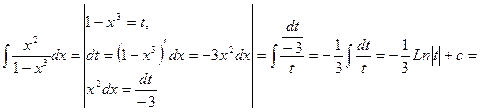


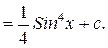
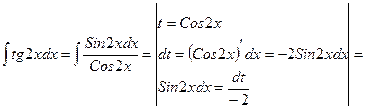
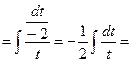
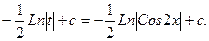
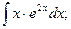 б)
б)  в)
в) 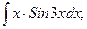
 (**)
(**)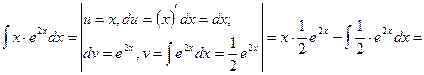

 найден методом подстановки t=2x.
найден методом подстановки t=2x.