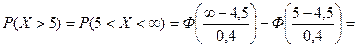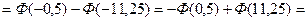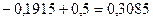Решение. Обозначим Х - случайная глубина посева семян.
Обозначим Х - случайная глубина посева семян. По условию 1. Доля семян посеянных на глубину более 5 см - это вероятность того, что случайно взятое семя будет посеяно на глубину более 5 см, т. е. это вероятность события Х >5. Определим эту вероятность. Здесь не указана наибольшая граница интервала, она может быть какой угодно. При решении задач ее принимают равной бесконечности, а функцию Лапласа Ф(∞)=0,5.
Таким образом, 10,56% семян посеяно на глубину более 5см.
2. Здесь нужно найти вероятность события Х<4,3. Так как не указана наименьшая граница интервала, то при решении задач ее принимают равной минус бесконечности. В нашей же задаче она равна нулю, т. к. речь идет о глубине посева семян. Тогда
Таким образом, 30,85 % семян посеяно на глубину менее 4,3 см. Вопросы для самопроверки
1.Сформулируйте определение случайной величины. 2.Какие случайные величины называются дискретными? (непрерывными?). Приведите примеры. 3. Что называется законом распределения случайной величины? 4. Как задается закон распределения дискретной случайной величины? 5. Дайте определение математического ожидания дискретной случайной величины. 6. Перечислите основные свойства математического ожидания. 7.Какое свойство случайной величины характеризует математическое ожидание? 8.Дайте определение дисперсии и среднего квадратического отклонения дискретной случайной величины. 9.Перечислите свойства дисперсии. 10.Дайте определение интегральной функции распределения. Перечислите ее свойства. 11.Дайте определение дифференциальной функции распределения. Перечислите ее свойства. 12.Что называется математическим ожиданием непрерывной случайной величины? Как оно вычисляется? 13.Как определяется дисперсия непрерывной случайной величины и как она вычисляется? 14. Какое распределение непрерывной случайной величины называется нормальным?
|