Начертите кривую нормального распределения. Как меняется кривая при изменении математического ожидания и среднего квадратического отклонения?
16.Как вычисляется вероятность попадания нормально распределенной случайной величины в заданный интервал? 17.Сформулируйте правило трех сигм. 18. Сформулируйте теорему Ляпунова. 19. В чем сущность закона больших чисел? 20. Сформулируйте теорему Бернулли. Какое значение имеет эта теорема для практики? 21. Сформулируйте теорему Чебышева. Укажите ее значение для практики?
Раздел 3. Задачи для контрольной работы №1
В задачах 1- 20 даны вершины треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнение стороны АВ; 3) уравнение высоты СD и ее длину; 4) уравнение окружности, для которой высота СD является диаметром. 1. А(-2;1), В(10;10), С(8;-4). 2. А(-4;-1), В(8;8), С(6;-6). 3. А(-1;0), В(11;9), С(9;-5). 4. А(-3;-3), В(9;6), С(7;-8). 5. А(-3;0), В(9;9), С(7;-5). 6. А(-5;-2), В(7;7), С(5;-7). 7. А(-2;-1), В(10;8), С(8;-6). 8. А(-5;1), В(7;10), С(5;-4). 9. А(-2;-3),В(10;6),С(8;-8). 10. А(-6;1), В(6;10),С(4;-4). 11. А(3;0), В(-9;9), С(-7;-5). 12. А(0;1), В(-12;10), С(-10;-4). 13. А(4;-3), В(-8;6), С(-6;-8). 14. А(1;1), В(-11;10), С(-9;-4). 15. А(8;-2), В(-4;7), С(-2;-7). 16. А(6;2), В(-6;11), С(-4;-3). 17. А(2;-1), В(-10;8), С(-8;-6). 18. А(5;1), В(-7;10), С(-5;-4). 19. А(3;3), В(-9;12), С(-7;-2). 20. А(1;2), В(-11;11), С(-9;-3).
В задачах 21-40 найти пределы функций.
21 а) б) 22 а) б) 23 а) б) 24 а) б) 25 а) б) 26 а) б) 27 а) б) 28 а) б) 29 а) б) 30 а)
б)
31 а)
б)
32 а)
б)
33 а)
б)
34 а)
б)
35 а)
б)
36 а)
б)
37 а)
б)
38 а)
б)
39 а)
б)
40 а)
б)
В задачах 41-60 найти производные данных функций.
41. а) в) 42. а) в) 43. а) в) 44. а) в) 45. а) в) 46. а) в) 47. а) в) 48. а) в) 49. а) в) 50. а) в) 51. а) в) 52. а) в) 53. а) в) 54. а) в) 55. а) в) 56.а) в) 57. а) в) 58. а) в) 59. а) в) 60. а) в)
В задачах 61-80 исследовать данные функции методами дифференциального исчисления и построить их графики. При исследовании функции следует найти ее интервалы возрастания и убывания и точки экстремума, интервалы выпуклости и вогнутости и точки перегиба графика функции. 61. у=х3-9х2+24х-13. 62. у=х3-6х2+9х+1. 63. у=х3-3х+1. 64. у=х3-3х2+6. 65. у=х3+3х2-1. 66. у=х3+6х2+9х+1. 67. у=х3-12х2+45х-48. 68. у=х3-9х2+24-17. 69. у=х3+6х2+9х+2. 70. у=х3-12х2+45х-47. 71. у=-х3+3х2-5. 72. у= -х3+9х2-24х+18. 73. у= -х3-6х2-9х-3. 74. у= - х3+3х-5. 75. у= -х3+12х2-45+53. 76. у=-х3-9х2-24х-21. 77. у=-х3+15х2-72х+109. 78. у=-х3-3х2-2. 79. у=-х3+18х2-105х+195. 80. у=-х3+9х2-24+14.
В задачах 81-100 вычислить неопределенные интегралы и результаты интегрирования проверить дифференцированием. 81. а) б) 82. а) б) 83. а) б) 84. а) б) 85 а) б) 86. а) б) 87. а) б) 88. а) б) 89. а) б) 90. а) б) 91. а) б) 92. а) б) 93. а) б) 94. а) б) 95. а) б) 96. а) б) 97. а) б) 98. а) б) 99. а) б) 100. а) б)
В задачах 101-120 вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж. 101. у=х2-4х+3, у=х-1 102. у=х2+2х, у=х+2 103. у=х2+4х+3, у=х+3. 104. у=х2-6х+10, у=х. 105. у=х2-2х-1, у=х-1. 106. у=х2+6х+8, у=х+4. 107. у=х2-6х+13, у=х+3. 108. у=х2+8х+15, у=х+5. 109. у=х2, у=х+2. 110. у=х2-1, у=х+1. 111. у=х2-6х+8, у=х-2. 112. у=х2-3х, у=х-1. 113. у=х2-4х-5, у=0,5х. 114. у=х2+х-2, у=2х. 115. у=х2-4х+8, у=х+2. 116. у=1-х2, у=0. 117. у=4-х2, у=0. 118. у=2х2, у=2х+4. 119. у=6х-х2, у=0. 120. у=3х2-3, у=-х.
В задачах 121-140 решить систему линейных уравнений методом Крамера и сделать проверку. 121. 122. 123. 124. 125. 126. 127. 128. 129. 130.
|

 в)
в) 
 г)
г) 
 в)
в) 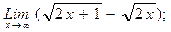
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 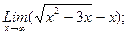
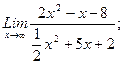 г)
г) 
 в)
в) 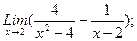
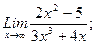 г)
г) 
 в)
в) 
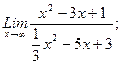 г)
г) 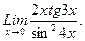
 в)
в) 
 г)
г) 
 в)
в) 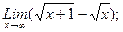
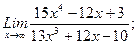 г)
г) 
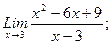 в)
в) 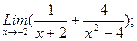
 г)
г) 
 в)
в) 
 г)
г) 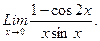
 в)
в) 
 г)
г) 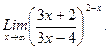
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
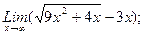 г)
г) 
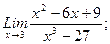 в)
в) 
 г)
г) 
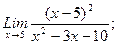 в)
в) 
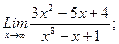 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 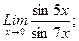
 г)
г) 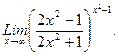
 б)
б) 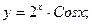
 г)
г) 
 б)
б) 
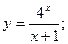 г)
г) 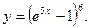
 б)
б) 
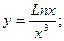 г)
г) 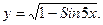
 б)
б) 
 г)
г) 
 б)
б) 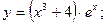
 г)
г) 
 б)
б) 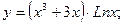
 г)
г) 
 б)
б) 
 г)
г) 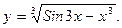
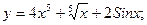 б)
б) 

 б)
б) 
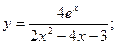 г)
г) 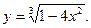
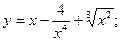 б)
б) 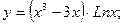
 г)
г) 
 б)
б) 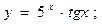
 г)
г) 
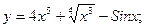 б)
б) 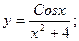 г)
г) 
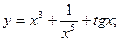 б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 
 б)
б) 

 г)
г) 
 б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 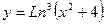
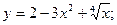 б)
б) 
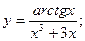 г)
г) 
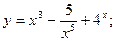 б)
б) 
 г)
г) 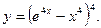

 в)
в) 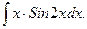

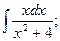 в)
в) 

 в)
в) 

 в)
в) 

 в)
в) 

 в)
в) 

 в)
в) 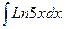
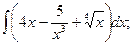
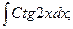 в)
в) 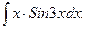

 в)
в) 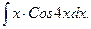

 в)
в) 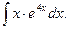

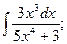 в)
в) 
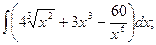
 в)
в) 

 в)
в) 

 в)
в) 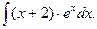
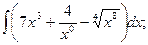
 в)
в) 
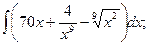
 в)
в) 

 в)
в) 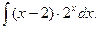

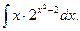 в)
в) 

 в)
в) 
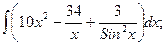
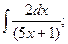 в)
в) 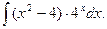
 131.
131. 
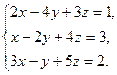 132.
132. 
 133.
133. 
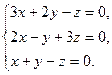 134.
134. 
 135.
135. 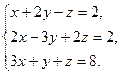
 136.
136. 
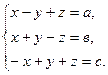
 138.
138. 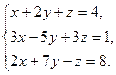
 139.
139. 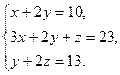
 140.
140. 



