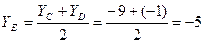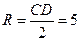Тема 1. Аналитическая геометрия на плоскости
Литература: [3] гл.1 §1, гл.3,4 [5], № 4,29,67,155,166 Разберите решение задач 1,2,3.
Задача 1. Даны вершины треугольника АВС: А(-2;-4), В(10;5), С(8;-9). Найти: 1. длину стороны АВ 2. уравнение стороны АВ 3. уравнение высоты СD и ее длину 4. уравнение окружности, для которой высота СD является диаметром.
Решение. 1. Расстояние d между точками М1 (x1; y1) и М2 (x2;y2) определяется по формуле:
Подставив в эту формулу координаты точек А и В, имеем:
2. Уравнение прямой, проходящей через точки М1 (x1; y1) и М2 (x2;y2), имеет вид:
Подставив в (2) координаты точек А и В, получим уравнение прямой АВ:
3. Высота CD перпендикулярна стороне АВ, поэтому угловые коэффициенты этих прямых обратные по величине и противоположные по знаку, т.е.
Для нахождения углового коэффициента относительно у: -4y=-3х+10, отсюда Тогда из (3) находим:
Уравнение прямой, проходящей через точку М1 (x1; y1) в заданном угловым коэффициентом k направлении, имеет вид:
Подставив в (4) координаты точки С и
Для нахождении длины отрезка СD определим координаты точки D. Решим систему уравнений прямых АB и СD методом сложения:
Итак, D (2;-1).
Подставив в формулу (1) координаты точек C и D имеем,
4. Уравнение окружности радиуса R с центром в точке Е (a; b) имеет следующий вид:
Так как CD является диаметром искомой окружности, то ее центр E есть середина отрезка CD. По формулам деления отрезка пополам, получаем:
Следовательно, Е(5;—5) и По формуле (5) получаем уравнение окружности: (x-5)2+(y+5)2=25
На рисунке 1 в декартовой прямоугольной системе координат хОу изображены треугольник ABC, высота СD, окружность радиуса 5 единиц с центром в точке Е.
рис. 1
Вопросы для самопроверки
1. Что называется прямоугольной системой координат? 2. Напишите формулу для нахождения расстояния между двумя точками. 3. Напишите формулы для определения координат точки, делящей отрезок: а) в данном отношении; б) пополам. 4. Напишите уравнения прямой: а) с угловым коэффициентом; б) проходящей через данную точку в данном направлении; в) проходящей через две данные точки. 5. Как найти координаты точки пересечения двух прямых? 6. Напишите формулу для определения угла между двумя прямыми. 7. Сформулируйте условия параллельности и перпендикулярности двух прямых. 8. Что называется окружностью? 9. Напишите уравнение окружности с центром в произвольной точке плоскости хОу; с центром в начале координат.
|

 (1)
(1)
 (2)
(2)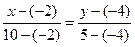




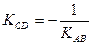 (3)
(3) прямой АВ, разрешим уравнение этой прямой
прямой АВ, разрешим уравнение этой прямой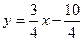

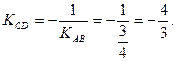
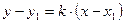 (4)
(4) , получим уравнение высоты CD:
, получим уравнение высоты CD: 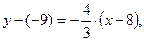 ,
,  ,
, 

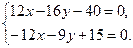
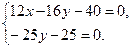

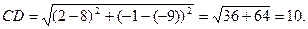
 (5)
(5)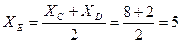 ,
,