Расчет термодинамических характеристик сплава по диаграмме состояния
– Задача. По диаграмме состояния системы Fe–Mn рассчитать теплоты растворения и коэффициенты активности марганца и железа в расплаве Fe–Mn с атомным содержанием марганца 30 % при 1673 К, использовав ТРР. – Исходные данные. 1. Диаграмма состояния Fe–Mn [13] (см. рисунок). 2. Температура и теплота плавления марганца и железа: T пл (Мn) = 1517 К, D H пл (Мn) = 14,6 кДж/моль, T пл (Fe) = 1809 К, D H пл (Fe) = 15,2 кДж/моль. – Теория. В жидко-твердой области химические потенциалы компонентов в жидкой и твердой фазах при температуре Т, соответствующие равновесию фаз, одинаковы:
– В качестве стандартного состояния выбираем чистый компонент i в жидком и твердом состояниях соответственно для жидкой
– и аi = g iхi, – получаем следующие уравнения для компонентов бинарного сплава:
– – В системе уравнений (1.46) неизвестны четыре коэффициента активности компонентов в жидкой и твердой фазах. Дляих определения необходимы еще два уравнения. Воспользуемся приближением ТРР, согласно которому D H 1 = RТ ln g1 = (1 - x 1)2W; (1.47) D H 2 = RТ ln g2 = (1 - x 2)2W, (1.48) – где W - энергия взаимообмена, является параметром теории. – С учетом выражений (1.47) и (1.48) уравнения (1.46) преобразуется к виду:
– Уравнения (1.49) и (1.50) содержат две неизвестные величины и легко разрешаются относительно W(ж) и W(тв). – Решение. Из диаграммы состояния системы Fe–Mn видно, что сплав с атомным содержанием марганца 30 % кристаллизуется в диапозоне температур 1685–1663 К. Рассмотрим равновесие между жидкой и твердой фазами при 1673 К:
W(тв) = 2354 + 0,840×W(ж). – По уравнению (1.50) вычисляем энергию взаимообмена W(ж):
W(ж) = 4742 Дж/моль. – Теплоты растворения и коэффициенты активности марганца и железа в расплаве Fe–Mn (х Mn = 0,3) при 1873 К находим по уравнениям (1.47) и (1.48): – D H Mn = (1 - x Mn)2W = (1 - 0,3)2×4742 = 2324 Дж/моль; – ln gMn = (1 - x Mn)2W / RT = 2324/(8,31×1873) = 0,149; gMn = 1,16; – D H Fe = (1 - x Fe)2 W = (1 - 0,7)2×4742 = 427 Дж/моль; – ln gFe = D H Fe / RT = 427/(8,31×1873) = 0,0274; gFe = 1,03. – Примечания. 1. Расчет правильно предсказывает положительные отклонения системы Fe–Mn от закона Рауля. – 2. Термодинамический метод часто используется для построения диаграммы состояния. – 3. Область применения ТРР ограничена системами, образующими непрерывный ряд твердых растворов. В общем случае описанный метод расчета термодинамических величин является приближенным и может быть рекомендован только для оценочных расчетов при отсутствии экспериментальных данных.
|

 .
.
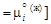 и твердой
и твердой 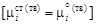 фаз. Учитывая, что
фаз. Учитывая, что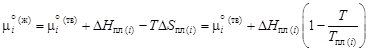
 (1.46)
(1.46) Температура T в двухфазной области и соответствующие ей составы равновесных фаз (точки
Температура T в двухфазной области и соответствующие ей составы равновесных фаз (точки  и
и 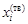 ) определяются из диаграммы состояния (см. рисунок).
) определяются из диаграммы состояния (см. рисунок).
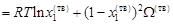 , (1.49)
, (1.49)
 . (1.50)
. (1.50)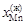 = 0,335;
= 0,335; 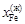 = 0,665;
= 0,665; 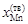 = 0,275;
= 0,275;  = 0,725. Подставив исходные данные в уравнение (1.49), получим
= 0,725. Подставив исходные данные в уравнение (1.49), получим






