Расчет стандартной энергии Гиббса и константы равновесия химической реакции по справочным данным
– Задача. С помощью справочных таблиц определить стандартную энергию Гиббса и константу равновесия реакции восстановления хрома кремнием при 1873 К: 2(Cr2O3) + 3[Si] = 4[Cr] + 3(SiO2). (1.33) – Исходные данные. 1. Значения стандартной энергии Гиббса образования соединений (Дж/моль) заданы в виде: 1) табличных данных при 1873 К [8]: – 2. Теплота образования диоксида кремния и триоксида дихрома при 0 К [9], Дж/моль: – Теория. Стандартной энергией Гиббса химической реакции D G º называют изменение энергии Гиббса системы в результате протекания реакции при условии, что исходные вещества и продукты реакции взяты в стандартных состояниях. – Для кремния, температура плавления которого меньше заданной, за стандартное состояние примем чистый жидкий кремний. Температура плавления остальных компонентов, участвующих в реакции (1.33), превышает 1873 К, поэтому для них в качестве стандартного примем твердое состояние. При таком выборе стандартных состояний стандартная энергия Гиббса D G º равна изменению энергии Гиббса в результате реакции 2Сr2O3 (тв) + 3Si(ж) = 4Cr(тв) + 3SiO2 (тв). (1.34) – Реакцию (1.34) можно представить как сумму двух процессов: 2Сr2O3 (тв) = 4Сr(тв) + 3O2 (г); (1.35) 3Si(ж) + 3O2 (г) = 3SiO2 (тв). (1.36) – Так что f ° (Т) = -[ G° (Т) - – где – Расчет констант равновесия с использованием приведенных энергий Гиббса (случай 3) проводится по уравнению R ln K = Df ° (Т) – – где Df ° (Т)- изменение приведенной энергии Гиббса в результате протекания реакции. – Решение. По исходным данным определяем стандартные энергии образования твердого диоксида кремния и кристаллического триоксида дихрома. – 1. Из таблиц [8] имеем: – 2. В соответствии с приведенными уравнениями
– 3. По данным о приведенных энергиях Гиббса [9] находим
– Используя уравнение (1.37) и исходные данные о теплотах образования оксидов при 0 К, получаем
– Стандартная энергия Гиббса реакции восстановления хрома кремнием [уравнение (1.34)]
– Подстановка найденных по разным данным значений – 1) D G ° = 2×651079 - 3×542070 = -324052 Дж/моль; K = 9,8×1010 ; – 2) D G ° = 2×662750 - 3×576146 = -402938 Дж/моль; K = 1,73×1011 ; – 3) D G ° = 2×636035 - 3×563520 = -418490 Дж/моль; K = 2,10×1012 . – Примечания. 1. Рассчитанные разными способами значения D G o заметно различаются. Это связано с точностью определения величин – 2. В некоторых справочных таблицах даны приведенные потенциалы веществ не при 0 К, а при 298 К. В этом случае
– где 11. Расчет термодинамических свойств бинарных расплавов в приближении – Задача. В приближении ТРР рассчитать коэффициенты активности ванадия и железа, парциальные и интегральные энтальпии, энтропии и энергии Гиббса расплавов Fe–V по данным о начальной теплоте растворения ванадия в железе. – Исходные данные. Начальная теплота растворения ванадия в жидком железе при 1873 К: – Теория. В ТРР предполагается, что отклонение раствора от совершенного обусловлено только энтальпийным членом (D Hm ¹ 0), а энтропия регулярного раствора такая же, как совершенного (
– В ТРР энтальпия определяется уравнениями
– где W - энергия взаимообмена (смешения), является параметром теории W = - zNA [e1, 2 - – NA - число Авогадро; e i , j - энергия взаимодействия между атомами i и j, расположенными в соседних узлах квазирешетки с координационным числом z. – Энергия Гиббса в ТРР равна D Gm = D Hm – T D Sm = х 1 x 2W + RТ (x 1ln х 1 + x 2ln х 2); D Gi = D Hi – T D Si = (1 - хi)2W + RТ ln хi;
– Отсюда lng i = (1 – хi)2W/ RТ. (1.39) – Таким образом, для расчета термодинамических характеристик бинарного расплава в приближении ТРР необходимо знать параметр W. Как правило, его определяют по экспериментальным данным, используя уравнения (1.38) или (1.39). – Решение. Для определения энергии взаимообмена в расплаве Fе–V воспользуемся исходными данными о величине – D Hm = x Fe x VW = -0,9×0,1×48073 = -4326 Дж/моль; – D H V = (1 - x V)2W = -(1 - 0,1)2×48073 = -38939 Дж/моль; – D H Fe = (1 - x Fe)2W = -(1 - 0,9)2×48073 = -481 Дж/моль; – lngV =D H V/ RT = -38393/(8,314×1873) = -2,50; gV = 0,082; – lngFe = D H Fe/ RT = -481/(8,314×1873) = -0,031; gFe = 0,970; – D Sm = - R (x Vln x V + x Feln x Fe) = -8,314 (0,1 ln0,1 + 0,9ln0,9) = – D S V = - R ln x V = -8,314 ln0,1 = 19,147 Дж/(моль×К); – D S Fe = - R ln x Fe = -8,314 ln0,9 = 0,876 Дж/(моль×К); – D Gm = D Hm - T D Sm = 4326 - 1873×2,70 = -9402 Дж/моль; – D G V = D H V - T D S V = -38939 - 1873×19,15 = -74804 Дж/моль; – D G Fe = D H Fe - T D S Fe = -481 - 1873×0,88 = -2129 Дж/моль. – Результаты расчета концентрационных зависимостей термодинамических свойств расплава Fе–V в сопоставлении с экспериментальными данными [10] приведены в таблице. Результаты расчета термодинамических свойств расплавов Fе–V при 1873 К
– Примечания. 1. Термин «регулярные растворы» не связан с существом модели [3]. Он введен Гильдебрандом для обозначения семейства растворов, характеризующихся определенной закономерностью (регулярностью) изменения ряда свойств. Оказалось, что рассмотренная модель удовлетворительно описывает свойства таких растворов. В результате и сама модель получила название регулярного раствора. – 2. Величина параметра W в ТРР может быть определена различными способами: по известной экспериментальной теплоте образования расплава, по данным об энергии Гиббса расплава или коэффициенте активности одного из компонентов. Значения W, рассчитанные с помощью различных термодинамических величин, могут заметно различаться. Так, при определении W по экспериментальной теплоте образования расплава эквиатомного состава (x V = x Fe = 0,5) D Hm = -9162 Дж/моль, получим W = -36648 Дж/моль. Расчет W по значениям коэффициента активности ванадия при x V = 0,5, gV = 0,64 дает W = -6942 Дж/моль. Различие результатов расчета является следствием отклонения системы Fe–V от регулярных растворов. – 3. В приближении ТРР кривые, описывающие термодинамические свойства бинарных расплавов в зависимости от состава, симметричны относительно точки х 1 = x 2 = 0,5. Экспериментальные концентрационные зависимости, как правило, асимметричны. Так, для расплавов Fe–V максимум термодинамических характеристик (их абсолютных величин) соответствует х V» 0,45. Асимметрия концентрационных зависимостей свойств учитывается в теории субрегулярных растворов (ТСР) [3]. В приближении ТСР предполагается, что энергия взаимообмена линейно зависит от состава: W = х 1 А 1 + х 2 А 2, где А 1 и A 2 - параметры, определяемые по экспериментальным значениям теплот растворения или коэффициентов активности компонентов. Дляих определения требуются две экспериментальные точки. В частности, значения А 1 и А 2 можно найти по данным о начальных теплотах растворения: А 1 = – 4. ТРР можно применять для систем с относительно слабым межатомным взаимодействием (например, Fe–Cr, Fe–Со, Ni–Со). Однако ТРР часто используют и для расплавов с сильным межатомным взаимодействием. Например в тех случаях, когда экспериментальные данные ограничены, так что можно рассчитать только один параметр W.
|

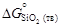 = -542070;
= -542070;  = -651079; 2) уравнений [3]:
= -651079; 2) уравнений [3]: 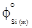 = 46,06;
= 46,06; 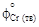 = = 51,86;
= = 51,86; 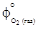 = 236,92;
= 236,92; 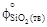 = 100,28;
= 100,28; 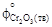 = 192,82.
= 192,82.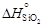 = -905717;
= -905717; 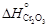 = -1134777.
= -1134777.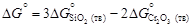 , где
, где 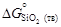 и
и 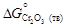 - стандартные энергии образования оксидов при 1873 К. Константа равновесия K определяется известным соотношением: D G o = - RТ ln К. Для определения энергии образования химических соединений из элементов по уравнениям (1.35) и (1.36) используют справочные таблицы (таблицы стандартных величин), которые составлены по-разному: 1) значения D G º (Т) приведены с определенным шагом по температуре (обычно 100 К); 2) приведены значения коэффициентов А и В, характеризующих температурную зависимость энергии Гиббса: D G º(Т) = А + ВТ, указаны температурные интервалы, в которых коэффициенты А и В принимают постоянными величинами, независимыми от температуры; 3) даны приведенные энергии Гиббса веществ fº(Т):
- стандартные энергии образования оксидов при 1873 К. Константа равновесия K определяется известным соотношением: D G o = - RТ ln К. Для определения энергии образования химических соединений из элементов по уравнениям (1.35) и (1.36) используют справочные таблицы (таблицы стандартных величин), которые составлены по-разному: 1) значения D G º (Т) приведены с определенным шагом по температуре (обычно 100 К); 2) приведены значения коэффициентов А и В, характеризующих температурную зависимость энергии Гиббса: D G º(Т) = А + ВТ, указаны температурные интервалы, в которых коэффициенты А и В принимают постоянными величинами, независимыми от температуры; 3) даны приведенные энергии Гиббса веществ fº(Т): ]/ T, (1.37)
]/ T, (1.37)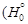 / T),
/ T),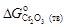 = -1131000 + 250,0 Т = -1131000 + 250,0×1873 = = -662750 Дж/моль.
= -1131000 + 250,0 Т = -1131000 + 250,0×1873 = = -662750 Дж/моль.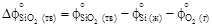 = 100,28 - 46,06 - 236,92 =
= 100,28 - 46,06 - 236,92 =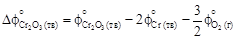 = 192,82 -
= 192,82 - ×236,92 = -266,28 Дж/(К×моль).
×236,92 = -266,28 Дж/(К×моль).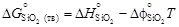 = -905717 + 182,7×1873 =
= -905717 + 182,7×1873 =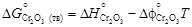 = -1134777 + 266,28×1873 =
= -1134777 + 266,28×1873 =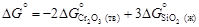 .
.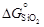 дает следующие результаты:
дает следующие результаты: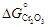 . По данным [8] при комнатной температуре она составляет ~ 2 кДж/моль для Сr2O3 и ~ 4 кДж/моль для SiO2. Более точными являются значения D G °, рассчитанные по данным [9] о приведенных потенциалах.
. По данным [8] при комнатной температуре она составляет ~ 2 кДж/моль для Сr2O3 и ~ 4 кДж/моль для SiO2. Более точными являются значения D G °, рассчитанные по данным [9] о приведенных потенциалах.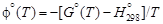 ,
,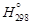 - энтальпия вещества при 298 К.
- энтальпия вещества при 298 К.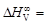 -48073 Дж/моль [10] (стандартное состояние – жидкий ванадий).
-48073 Дж/моль [10] (стандартное состояние – жидкий ванадий).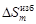 = 0), т.е. предполагается, что расположение атомов хаотично, как в идеальном растворе. Энтропия образования бинарного регулярного раствора
= 0), т.е. предполагается, что расположение атомов хаотично, как в идеальном растворе. Энтропия образования бинарного регулярного раствора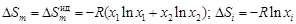 .
.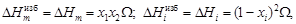 (1.38)
(1.38) (e1, 1 + e2, 2)];
(e1, 1 + e2, 2)];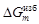 = D Hm = х 1 x 2W;
= D Hm = х 1 x 2W;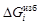 = RT lng i = D Hi = (1 – хi)2W.
= RT lng i = D Hi = (1 – хi)2W.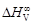 . В соответствии с уравнением (1.38) имеем: W =
. В соответствии с уравнением (1.38) имеем: W = 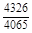
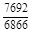
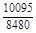
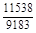
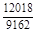
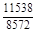
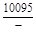
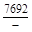
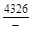
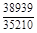
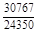
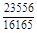
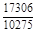
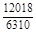
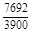
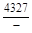
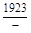
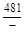
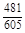
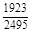
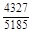
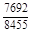
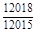
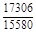
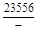
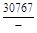
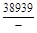
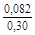
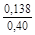
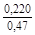
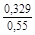
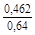
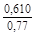
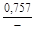
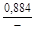
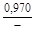
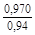
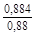
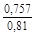
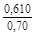
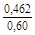
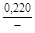
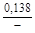
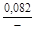
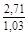
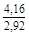
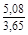
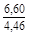
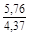
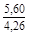
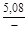
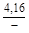
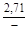
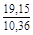
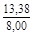
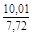
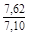
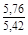
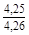
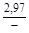
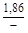
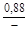
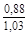
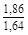
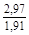
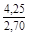
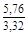
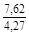
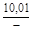
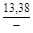
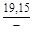
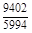
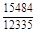
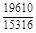
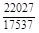
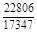
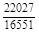
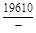
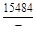

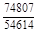
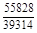
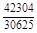
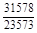
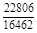
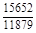
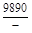
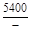
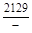
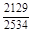
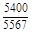
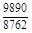

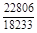
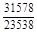
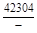
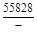
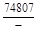
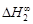 , A 2 =
, A 2 = 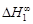 или коэффициентах активности А 1 = = RТ ln
или коэффициентах активности А 1 = = RТ ln 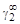 , А 2 = RТ ln
, А 2 = RТ ln 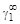 .
.


