Графическое определение параметров взаимодействия
– Задача. Графически определить параметры взаимодействия – Исходные данные. В расплавах Ni–Cr экспериментально определены [15] значения растворимости азота [N] при 1873 К и р N2= 1 атм в зависимости от концентрации хрома:
– Теория. Параметры взаимодействия являются коэффициентами ряда Тейлора, в который можно разложить логарифм коэффициента активности компонента раствора (lg fi) вблизи точки, соответствующей чистому растворителю [3]. Для рассматриваемых сплавов имеем
– В этой формуле
– Если имеется график зависимости lg f N от [% Cr], то параметр
– Чтобы найти значения lg f N по имеющимся данным о растворимостях [N], учтем, что все они относятся к одному давлению азота в газовой фазе. Отсюда следует, что активности азота во всех расплавах одинаковы: a N = f N[N] = const. При [Cr] = 0 коэффициент активности азота равен 1, так как f N в данном случае учитывает влияние хрома на a N. Отсюда a N = [N][Cr] = 0 и, следовательно,
– Решение. Найдем с помощью выражения (1.56) коэффициенты активности азота в заданных сплавах и их логарифмы:
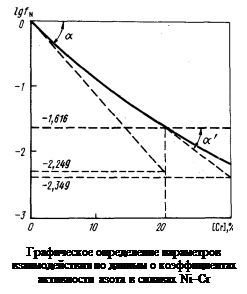
– Построим график зависимости lg f N от [% Cr] (см. рисунок). Проведем касательные к полученной кривой в точках, соответствующих содержанию хрома 0 и 20 %. Определим графически ординаты точек пересечения касательных с вертикалями 20 и 30 % Cr (эти ординаты показаны на рисунке). В результате получим
– В соответствии с уравнением (1.55)
–
16. Теоретическая оценка параметра – Задача. Зная коэффициент активности компонента g i, определить параметры взаимодействия – Исходные данные. Коэффициент активности меди в железе – Теория. Как показано в работе [3], концентрационная и температурная зависимость g i выражается в ТРР уравнением ln g i ( T ) = (W/ RT)(1 - xi)2, (1.60) – где W - энергия смешения, в простейшем варианте ТРР не зависящая ни от температуры, ни от концентрации. Дифференцируя уравнение (1.60) по хi и принимая хi ® 0, получаем
|

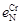 и
и 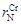 в жидком никеле при 1873 К по данным о растворимости азота в сплавах Ni–Cr.
в жидком никеле при 1873 К по данным о растворимости азота в сплавах Ni–Cr. (1.53)
(1.53)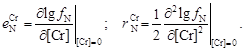 (1.54)
(1.54) как изменение тангенса угла наклона касательной, отнесенное к изменению [% Cr]:
как изменение тангенса угла наклона касательной, отнесенное к изменению [% Cr]: (1.55)
(1.55)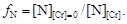 (1.56)
(1.56)
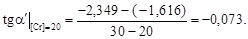
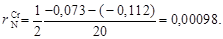
 Примечание. При использовании ЭВМ параметры взаимодействия
Примечание. При использовании ЭВМ параметры взаимодействия 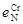 и
и  ;
;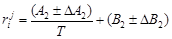 .
.
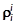 по
по 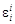 и
и  при 1873 К с помощью ТРР.
при 1873 К с помощью ТРР.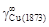 = 8,6 [3].
= 8,6 [3].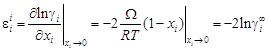 ; (1.61)
; (1.61) . (1.62)
. (1.62)


