Расчет коэффициентов активности компонентов бинарного раствора с помощью уравнения Гиббса – Дюгема
– Задача. С помощью уравнения Гиббса – Дюгема рассчитать коэффициент активности железа в расплавах Fе–Аl при 1873 К по экспериментальным значениям коэффициента активности алюминия. – Исходные данные. Зависимость коэффициента активности алюминия (gAl) от концентрации в расплавах Fе–Аl при 1873 К [6] приведена в таблице. Результаты расчета коэффициентов активности железа
– Теория. Парциальные термодинамические характеристики компонентов бинарного раствора связаны уравнением Гиббса – Дюгема. Для парциальных энергий Гиббса имеем: (1 – х 2)(¶ ln a 1/¶ х 2) T , р = - x 2(¶ ln a 2/¶ х 2) T , р . – Отсюда (1 – х 2)(¶ lng1/¶ х 2) T , р = - x 2(¶ lng2/¶ х 2) T , р . (1.30) – Таким образом, если известен коэффициент активности одного из компонентов, например g2, то с помощью уравнения (1.30) можно вычислить g1. Проинтегрировав уравнение (1.30), получим
– или
– Решение. Определение коэффициента активности железа в расплавах Fe–Аl по заданной концентрационной зависимости коэффициента активности алюминия сводится к вычислению интеграла (1.31). Воспользуемся графическим методом интегрирования. С этой целью строим график зависимости отношения x Аl/ x Fe от lngAl (см. рисунок). Заштрихованная на рисунке площадь равна интегралу
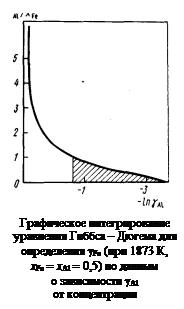 и значению lngFe при x Al = x Fe = 0,5. Рассчитанная таким образом концентрационная зависимость коэффициента активности железа приведена в таблице вмсте с исходными данными. и значению lngFe при x Al = x Fe = 0,5. Рассчитанная таким образом концентрационная зависимость коэффициента активности железа приведена в таблице вмсте с исходными данными.
– Примечания. 1. В области низких концентраций железа графическое интегрирование уравнения (1.31) затруднено по двум причинам. Во-первых, в этой области невысока точность определения величины gAl, во-вторых, отношение x Al/ x Fe ® ¥ при x Fe ® 0, поэтому при низких значениях х Fe (x Fe < 0,2; х Al > 0,8) коэффициенты активности железа получены экстраполяцией зависимости lngFe к точке x Fe = 0. – 2. Более удобное для расчета интегральное уравнение Гиббса – Дюгема может быть получено с помощью вспомогательной функции Даркена [7]: a2 = lng2/(1 - х 2)2. – Тогда
– В данном случае подынтегральное выражение ограничено во всем концентрационном интервале 0 £ x 2 £ 1. Функция aAl и результаты расчета концентрационной зависимости lngFe по уравнению (1.32) приведены в таблице. – 3. Более точно интегралы в уравнениях (1.31) и (1.32) можно вычислить численными методами (трапеций, Симпсона и др.) с помощью ЭВМ. – 4. Для ряда систем коэффициент активности g2 известен лишь в ограниченной области концентраций от
– Для расчета концентрационной зависимости gC по этому уравнению необходимо знать величину
|

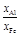
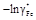
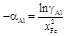
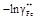
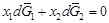 . Учитывая, что
. Учитывая, что 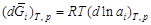 и dx 1 = - dx 2, это уравнение можно записать в виде
и dx 1 = - dx 2, это уравнение можно записать в виде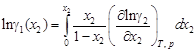
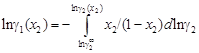 . (1.31)
. (1.31)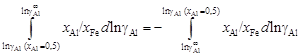
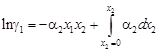 . (1.32)
. (1.32)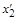 до
до 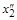 . Например, для системы Fе–С при 1873 К величина gFe известна в интервале 0,79 £ x Fe £ 1. В этом случае величину gC можно рассчитать по уравнению
. Например, для системы Fе–С при 1873 К величина gFe известна в интервале 0,79 £ x Fe £ 1. В этом случае величину gC можно рассчитать по уравнению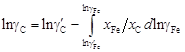 .
.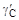 при x Fe = 0,79 (
при x Fe = 0,79 (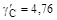 ).
).


