Расчет термодинамических свойств бинарных расплавов в приближении квазихимической модели (КХМ)
– Задача. Определить коэффициенты активности и теплоты растворения меди и железа в расплавах Fе–Cu, а также интегральные энтальпию, энтропию и энергию Гиббса при 1823 К по известному коэффициенту активности меди в бесконечно разбавленном растворе жидкого железа, используя КХМ. – Исходные данные. Коэффициент активности меди в жидком железе при 1823 К: – Теория. В отличие от ТРР и ТКР, КХМ учитывает упорядочение в расположении атомов. Предполагается, что число связей между атомами 1–1, 2–2 и 1–2 зависит от энергии межатомного взаимодействия. Если раствор образуется с выделением тепла, то преимущественно формируются связи 1–2. В случае, если теплота образования раствора > 0, разнородные атомы стремятся разделиться - число связей 1–1 и 2–2 превышает среднестатистическое. Это приводит к тому, что конфигурационная энтропия отличается от энтропии идеального, регулярного или квазирегулярного растворов, в которых расположение атомов считается хаотическим. – КХМ расплавов основана на квазикристаллической теории жидкости. В КХМ вводят параметр Х таким образом, чтобы произведение NA zХ (NA - число Авогадро, z – координационное число) равнялось числу пар атомов 1 и 2, занимающих соседние узлы квазикристаллической решетки (числу связей 1–2). Этот параметр связан с энергией взаимообмена W соотношением [12]:
– Очевидно, что для идеального раствора Х = x 1 x 2; Х > x 1 x 2, если W < 0 и Х < x 1 x 2, если W > 0. – Из уравнения (1.42) следует: Х = (2 x 1 x 2)/(1 + b), где
– Уравнения для расчета теплоты образования сплава и коэффициентов активности его компонентов в приближении КХМ имеют вид: D Нm = Х W = [(2 x 1 x 2)/(1 + b)]W; (1.44)
– Парциальные теплоты растворения компонентов можно рассчитать по уравнению
– где
– С помощью уравнений (1.44) и (1.45) можно определить интегральную энергию Гиббса и энтропию:
– Таким образом, для расчета термодинамических свойств бинарных расплавов в приближении КХМ необходимо знание двух параметров - энергии взаимообмена W и координационного числа z. – Решение. Для определения неизвестного параметра W воспользуемся заданным значением коэффициента активности меди в жидком железе при 1823 К
– откуда
– Рассчитаем термодинамические характеристики расплава Fe–Cu эквиатомного состава (x Fe = х Cu= 0,5). – Из уравнения (1.43) b = [1 + 4 x Fe x Cu(h2 - 1)]1/2 = [1 + 4×0,5×0,5(1,262 - 1)]1/2 = 1,26. – Тогда X = 2 x Fe x Cu/(1 + b) = 2×0,5×0,5/(1 + 1,26) = 0,221; D Hm = X W = 0,221×35049 = 7754 Дж/моль.
D H Fe = D H Cu = D Hm = 7754 Дж/моль; D Gm = RT [ x Feln(x Fe gFe) + x Culn(x Cu gCu)] = D Sm = (D Hm - D Gm)/ T = [7754 - (-2198)]/1823 = 5,46 Дж/(моль×К). – Результаты расчета концентрационных зависимостей термодинамических свойств расплавов Fe–Cu приведены в таблице. Результаты расчета термодинамических свойств расплавов Fе–Cu
– Примечания. 1. Рассчитанные по КХМ термодинамические характеристики расплавов Fe–Cu ближе к экспериментальным, чем результаты расчета по ТРР (за исключением энтропии) [3]. Однако использование КХМ, как и ТРР, приводит к ошибочному выводу о расслоении расплава на две несмешивающиеся жидкости. – 2. Избыточная энтропия, рассчитанная в приближении КХМ, всегда отрицательна (или равна нулю), так как конфигурационная энтропия не может превосходить энтропию идеального раствора с хаотическим расположением атомов. – 3. Название КХМ связано с законом действующих масс для реакции АА + ВВ = 2 АВ, поскольку константа реакции
|

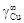 = 10,1; координационное число z = 10 [3].
= 10,1; координационное число z = 10 [3].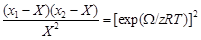 . (1.42)
. (1.42)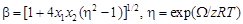 . (1.43)
. (1.43)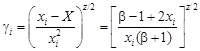 .(1.45)
.(1.45)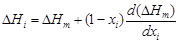 ,
,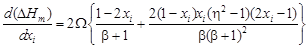 .
.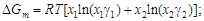
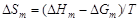 .
.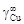 = 10,1. Энергию взаимообмена вычисляем с помощью уравнения (1.45). При хi ® 0, согласно уравнению (1.43), b ® 1. Подстановка х Cu = 0 и b = 1 в уравнение (1.45) дает неопределенность (0/0). Чтобы раскрыть ее, воспользуемся правилом Лопиталя: заменим предел отношения функций пределом отношения их производных. В результате получим
= 10,1. Энергию взаимообмена вычисляем с помощью уравнения (1.45). При хi ® 0, согласно уравнению (1.43), b ® 1. Подстановка х Cu = 0 и b = 1 в уравнение (1.45) дает неопределенность (0/0). Чтобы раскрыть ее, воспользуемся правилом Лопиталя: заменим предел отношения функций пределом отношения их производных. В результате получим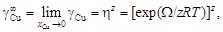
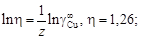
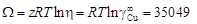 Дж/моль.
Дж/моль.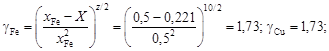
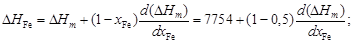
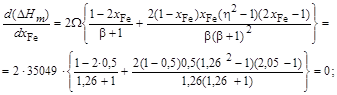
 dx Cu
dx Cu
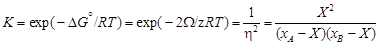 .
.


