Удаление неметаллических включений под действием гравитационных сил
– Задача. Рассчитать скорости всплывания неметаллических частиц в стали при 1873 К в гравитационном поле (конвективное перемешивание металла не учитывать). – Исходные данные. 1. Плотность глинозема rв= 3,97×103 кг/м3, жидкой при 1873 К силикатной частицы – Теория. Скорость подъема твердых сферических частиц в спокойной жидкости (Re < 1) определяется уравнением Стокса:
– где r - радиус частиц; rм и rв - плотность вещества среды и включения соответственно; hм - динамическая вязкость среды; g - ускорение свободного падения. – Эта формула получена приравниванием выталкивающей силы, действующей на частицу (сила Архимеда), и силы сопротивления движению в вязкой среде:
– Формула Стокса обычно применима вплоть до Re = 1. Поведение частиц размером менее 10-7 м (0,1 мкм) подчиняется преимущественно закономерностям броуновского движения. Скорость подъема жидких и газообразных сферических частиц в однокомпонентной жидкости определяется уравнением Рыбчинского – Адамара, полученного решением системы соответствующих дифференциальных уравнений:
– где hв - вязкость вещества частицы. – Очевидно, что для твердой частицы (hв >> hм) уравнение (1.79) переходит в формулу Стокса. – Решение. В случае всплывания твердых (при 1873 К) включений глинозема (Аl2О3) можно воспользоваться формулой (1.78). Частицы глинозема в металле, как правило, не имеют округлой формы, отклонение формы включений от сферической может заметно влиять на скорость их подъема. В случае одинакового объема наименьшее сопротивление испытывают округлые частицы. Для включений неправильной формы в знаменатель уравнения (1.78) вводят поправочный коэффициент k, равный для частиц А12О3 примерно 6. – Далее будет показано, в каком интервале скоростей движения включения размером 5×10-5 м (50 мкм) в спокойном металле выполняется формула (1.78), т.е. Re = (υd rм)/hм £ 1, где d - характеристический размер, равный диаметру частицы, υ; £ (Rehм)/(rм d) = (1×6×10-3)/(7,15×103×5×10-5) = 1,6×10-2 м/с. (1.80) – Скорость подъема частицы глинозема размером 10 мкм υ; = – В соответствии с неравенством (1.80) полученное значение скорости удовлетворяет условию Re < 1, и для частиц такого размера можно применять уравнение Стокса. Аналогичным образом подсчитываем скорости всплывания частиц размером 20 и 50 мкм, равные соответственно 0,2×10-4 и 1,3×10-4 м/с. – Рассчитаем теперь скорость всплывания жидкого (при 1873 К) силикатного включения размером 10 мкм по формуле (1.79): υ; = – Для частиц размерами 20 и 50 мкм по уравнению (1.79) получим соответственно скорости всплывания, равные 1,6×10-4 и 1×10-3 м/с. В случае силикатного включения hв >> hм и поправочный множитель в уравнении Рыбчинского – Адамара примерно равен 1/3, поэтому формула (1.79) переходит в формулу (1.78). Проведенный расчет показывает, что жидкие силикатные включения в спокойном металле всплывают несколько быстрее твердых частиц глинозема, что связано с их меньшей плотностью и сферической формой. – Примечание. В металлургических агрегатах в условиях интенсивного перемешивания металла доставка неметаллических включений к поверхности ванны осуществляется преимущественно конвективными потоками. Гравитационные силы в основном играют роль при переходе частиц через тонкий слой металла, непосредственно прилегающий к границе раздела металл–шлак, где вертикальная составляющая скорости конвективных потоков практически равна нулю.
|

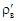 = 2,5×103 кг/м3, стали
= 2,5×103 кг/м3, стали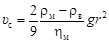 , (1.78)
, (1.78)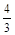 p r 3 g (rм – rв) = 6p r hм υ;.
p r 3 g (rм – rв) = 6p r hм υ;.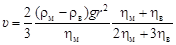 , (1.79)
, (1.79) = 0,5×10-5 м/с.
= 0,5×10-5 м/с. = 4×10-5 м/с.
= 4×10-5 м/с.


