Теорема сравнения и ее следствие применимы только к неотрицательным функциям. Как исследуется на сходимость несобственный интеграл 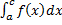 в случае функции
в случае функции 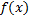 , меняющей знак на полуинтервале
, меняющей знак на полуинтервале 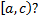 Заметим, что если от функции
Заметим, что если от функции 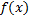 перейти к ее модулю
перейти к ее модулю 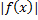 , то условие неотрицательности будет соблюдено.
, то условие неотрицательности будет соблюдено.
Предложение. Если интеграл от модуля функции сходится, то и интеграл от самой функции также сходится.
Доказательство. Итак, нам известно, что интеграл 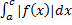 сходится. Из неравенств
сходится. Из неравенств 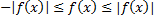 следует
следует 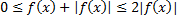 (прибавили ко всем частям величину
(прибавили ко всем частям величину 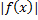 ). Из сходимости
). Из сходимости 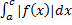 вытекает сходимость
вытекает сходимость 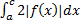 (свойство линейности). Тогда по теореме сравнения получаем, что и интеграл
(свойство линейности). Тогда по теореме сравнения получаем, что и интеграл 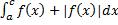 сходится. Разность двух сходящихся интегралов
сходится. Разность двух сходящихся интегралов 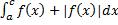 и
и  дает сходящийся интеграл
дает сходящийся интеграл 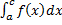 , что и требовалось доказать. □
, что и требовалось доказать. □
Определение. Несобственный интеграл 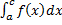 называется абсолютно сходящимся, если интеграл
называется абсолютно сходящимся, если интеграл 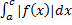 сходится. В случае, когда несобственный интеграл
сходится. В случае, когда несобственный интеграл 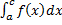 сходится, но не сходится абсолютно, то интеграл
сходится, но не сходится абсолютно, то интеграл 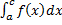 называют условно сходящимся.
называют условно сходящимся.
Пример. Интеграл 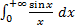 сходится условно. Обозначим
сходится условно. Обозначим 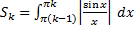 Геометрический аналог этого утверждения заключается в том, что суммарная площадь
Геометрический аналог этого утверждения заключается в том, что суммарная площадь 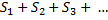 равна бесконечности, хотя знакочередующийся ряд
равна бесконечности, хотя знакочередующийся ряд 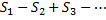 сходится (см. рис. 2).
сходится (см. рис. 2).
| Рис. 2. Условно сходящийся интеграл.
|
Действительно, для ε >0 имеем:
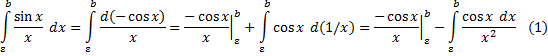
Так как 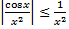 и интеграл
и интеграл 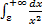 сходится, то при
сходится, то при 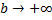 правая часть в (1) имеет предел. Следовательно, и левая часть
правая часть в (1) имеет предел. Следовательно, и левая часть 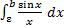 имеет предел при
имеет предел при 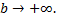 Итак, интеграл
Итак, интеграл 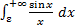 сходится. Точка 0 есть устранимая особенность функции
сходится. Точка 0 есть устранимая особенность функции 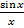 в силу первого замечательного предела. Доопределяя эту функцию в нуле единицей, получаем непрерывную функцию на отрезке
в силу первого замечательного предела. Доопределяя эту функцию в нуле единицей, получаем непрерывную функцию на отрезке 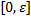 . Тем самым интеграл
. Тем самым интеграл 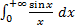 сходится в силу аддитивности несобственных интегралов.
сходится в силу аддитивности несобственных интегралов.
Докажем, что интеграл 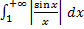 расходится. Предположим противное – он сходится. Тогда замена
расходится. Предположим противное – он сходится. Тогда замена 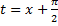 и эквивалентность
и эквивалентность 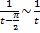 на бесконечности показывают, что и интеграл
на бесконечности показывают, что и интеграл 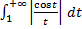 будет сходится. Так как
будет сходится. Так как
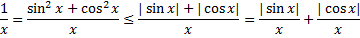
то по теореме сравнения получается, что интеграл 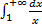 также сходится, что противоречит утверждению об эталонных интегралах.
также сходится, что противоречит утверждению об эталонных интегралах.

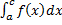 в случае функции
в случае функции 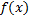 , меняющей знак на полуинтервале
, меняющей знак на полуинтервале 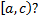 Заметим, что если от функции
Заметим, что если от функции 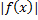 , то условие неотрицательности будет соблюдено.
, то условие неотрицательности будет соблюдено.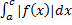 сходится. Из неравенств
сходится. Из неравенств 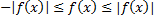 следует
следует 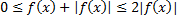 (прибавили ко всем частям величину
(прибавили ко всем частям величину 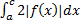 (свойство линейности). Тогда по теореме сравнения получаем, что и интеграл
(свойство линейности). Тогда по теореме сравнения получаем, что и интеграл 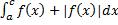 сходится. Разность двух сходящихся интегралов
сходится. Разность двух сходящихся интегралов  дает сходящийся интеграл
дает сходящийся интеграл 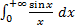 сходится условно. Обозначим
сходится условно. Обозначим 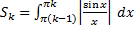 Геометрический аналог этого утверждения заключается в том, что суммарная площадь
Геометрический аналог этого утверждения заключается в том, что суммарная площадь 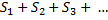 равна бесконечности, хотя знакочередующийся ряд
равна бесконечности, хотя знакочередующийся ряд 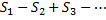 сходится (см. рис. 2).
сходится (см. рис. 2).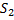
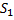
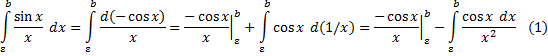
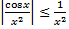 и интеграл
и интеграл 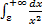 сходится, то при
сходится, то при 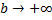 правая часть в (1) имеет предел. Следовательно, и левая часть
правая часть в (1) имеет предел. Следовательно, и левая часть 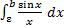 имеет предел при
имеет предел при 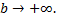 Итак, интеграл
Итак, интеграл 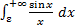 сходится. Точка 0 есть устранимая особенность функции
сходится. Точка 0 есть устранимая особенность функции 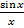 в силу первого замечательного предела. Доопределяя эту функцию в нуле единицей, получаем непрерывную функцию на отрезке
в силу первого замечательного предела. Доопределяя эту функцию в нуле единицей, получаем непрерывную функцию на отрезке 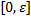 . Тем самым интеграл
. Тем самым интеграл 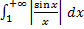 расходится. Предположим противное – он сходится. Тогда замена
расходится. Предположим противное – он сходится. Тогда замена 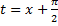 и эквивалентность
и эквивалентность 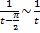 на бесконечности показывают, что и интеграл
на бесконечности показывают, что и интеграл 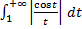 будет сходится. Так как
будет сходится. Так как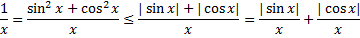
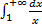 также сходится, что противоречит утверждению об эталонных интегралах.
также сходится, что противоречит утверждению об эталонных интегралах.


