Интеграл вида
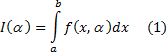
называется интегралом, зависящий от параметра a. В общем случае нижний и верхний пределы также могут зависеть от параметра a: a=a(a), b=b(a).
Теорема Лейбница дифференцирования по параметру. Пусть 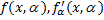 определены и непрерывны при a≤ x≤ b, c≤ a ≤ d. Тогда
определены и непрерывны при a≤ x≤ b, c≤ a ≤ d. Тогда
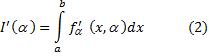
для любого a ∈ (c,d).
Доказательство. Применим теорему Лагранжа:
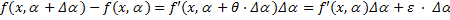
Здесь 0<θ <1 - зависит от  , а
, а  -- бесконечно малая величина при Δa → 0. Тогда
-- бесконечно малая величина при Δa → 0. Тогда

Лемма. Пусть  . Тогда
. Тогда  -- бесконечно малая величина при Δa → 0.
-- бесконечно малая величина при Δa → 0.
Доказательство леммы. Фиксируем положительное число δ. Для каждого 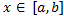 найдем
найдем  такое, что
такое, что 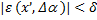 для всех пар
для всех пар  таких, что
таких, что
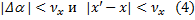
Пользуемся здесь тем, что  . Окрестности
. Окрестности 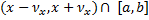 покрывают отрезок [a,b]. Выберем из них конечную систему с центрами в точках
покрывают отрезок [a,b]. Выберем из них конечную систему с центрами в точках  (см. раздел «Введение в анализ»). Тогда для
(см. раздел «Введение в анализ»). Тогда для 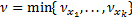 выполняется неравенство
выполняется неравенство 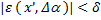 при любом
при любом  и любом
и любом 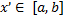 . Действительно,
. Действительно, 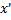 принадлежит одной из окрестностей
принадлежит одной из окрестностей 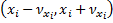 , а поэтому для пары
, а поэтому для пары  выполняется (4) при
выполняется (4) при  . Следовательно,
. Следовательно,
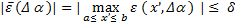
при любом 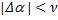 . Это и завершает доказательство леммы.
. Это и завершает доказательство леммы.
Продолжим доказательство теоремы. Так как
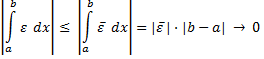
при 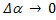 по лемме, то, переходя к пределу Δa → 0 в равенстве (3), получаем результат.□
по лемме, то, переходя к пределу Δa → 0 в равенстве (3), получаем результат.□
Следствие. Общая формула дифференцирования по параметру:
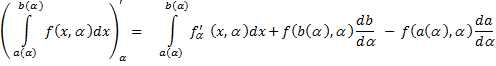
Пример. Обозначим  . Тогда
. Тогда 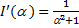 , откуда
, откуда  . Замена
. Замена  сводит этот интеграл к интегралу вида
сводит этот интеграл к интегралу вида  . Полагая здесь
. Полагая здесь  , получаем Интеграл Дирихле:
, получаем Интеграл Дирихле:


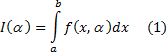
 определены и непрерывны при a≤ x≤ b, c≤ a ≤ d. Тогда
определены и непрерывны при a≤ x≤ b, c≤ a ≤ d. Тогда
 , а
, а  -- бесконечно малая величина при Δa → 0. Тогда
-- бесконечно малая величина при Δa → 0. Тогда
 . Тогда
. Тогда  -- бесконечно малая величина при Δa → 0.
-- бесконечно малая величина при Δa → 0. найдем
найдем  такое, что
такое, что 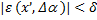 для всех пар
для всех пар  таких, что
таких, что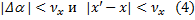
 . Окрестности
. Окрестности 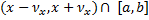 покрывают отрезок [a,b]. Выберем из них конечную систему с центрами в точках
покрывают отрезок [a,b]. Выберем из них конечную систему с центрами в точках  (см. раздел «Введение в анализ»). Тогда для
(см. раздел «Введение в анализ»). Тогда для 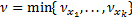 выполняется неравенство
выполняется неравенство 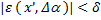 при любом
при любом  и любом
и любом 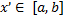 . Действительно,
. Действительно, 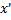 принадлежит одной из окрестностей
принадлежит одной из окрестностей 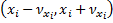 , а поэтому для пары
, а поэтому для пары  . Следовательно,
. Следовательно,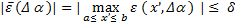
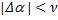 . Это и завершает доказательство леммы.
. Это и завершает доказательство леммы.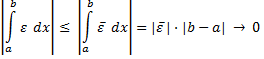
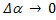 по лемме, то, переходя к пределу Δa → 0 в равенстве (3), получаем результат.□
по лемме, то, переходя к пределу Δa → 0 в равенстве (3), получаем результат.□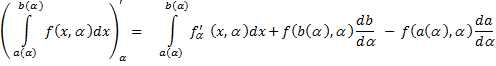
 . Тогда
. Тогда 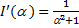 , откуда
, откуда  . Замена
. Замена  сводит этот интеграл к интегралу вида
сводит этот интеграл к интегралу вида  . Полагая здесь
. Полагая здесь  , получаем Интеграл Дирихле:
, получаем Интеграл Дирихле:



