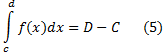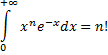Пусть функция 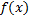 задана на полуинтервале
задана на полуинтервале 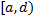 , где
, где 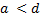 , а величина
, а величина 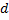 может быть как конечным числом, так и
может быть как конечным числом, так и  . Предположим, что
. Предположим, что 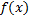 интегрируема на любом отрезке
интегрируема на любом отрезке 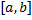 ,
, 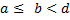 . Полагаем по определению
. Полагаем по определению
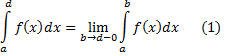
и называем это число несобственным интегралом. В случае, когда предел (1) существует, то говорим, что соответствующий интеграл сходится; в противном случае будем говорить, что он расходится.
Несобственный интеграл (1) применяется в двух типичных ситуациях.
1) Пусть 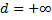 . Тогда
. Тогда 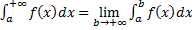
2) Пусть d∈ ℝ и функция 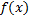 неограничена на полуинтервале
неограничена на полуинтервале 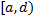 .
.
Если 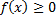 на полуинтервале
на полуинтервале 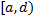 , то несобственный интеграл равен площади неограниченной фигуры -- криволинейной трапеции, ограниченной сверху графиком функции
, то несобственный интеграл равен площади неограниченной фигуры -- криволинейной трапеции, ограниченной сверху графиком функции 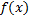 , снизу – осью Ох и слева – вертикальной прямой
, снизу – осью Ох и слева – вертикальной прямой  (см. рис. 1)
(см. рис. 1)
Рис.1 Несобственный интеграл 
|
Отметим, что если функция 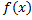 на самом деле интегрируема на отрезке
на самом деле интегрируема на отрезке 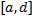 (это означает, в частности, что
(это означает, в частности, что 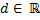 ), то коллизии обозначений не возникает -- несобственный интеграл в смысле (1) будет равен определенному интегралу функции
), то коллизии обозначений не возникает -- несобственный интеграл в смысле (1) будет равен определенному интегралу функции  на отрезке
на отрезке 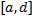 .
.
Аналогично определяется несобственный интеграл для функций, определенных на полуинтервале  , где
, где 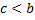 и
и  :
:
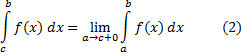
В примере § 16 мы фактически вычислили несобственный интеграл 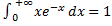 .
.
Cвойство линейности несобственных интегралов. Если интегралы  сходятся, то для любых чисел k и m сходится также и интеграл
сходятся, то для любых чисел k и m сходится также и интеграл 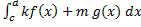 , и он равен
, и он равен 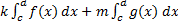 .
.
Это свойство вытекает из свойства линейности предельного перехода.
Свойство аддитивности несобственных интегралов. Пусть 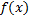 интегрируема на отрезке
интегрируема на отрезке 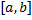 для фиксированного
для фиксированного 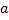 и любого
и любого  такого, что
такого, что 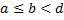 . Выберем точку
. Выберем точку 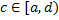 . Несобственный интеграл
. Несобственный интеграл  сходится в том и только том случае, если сходится несобственный интеграл
сходится в том и только том случае, если сходится несобственный интеграл 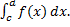 При этом условии имеет место равенство
При этом условии имеет место равенство

Формула Ньютона-Лейбница для несобственных интегралов. Пусть  -- первообразная непрерывной функции
-- первообразная непрерывной функции 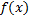 на интервале (c,d). Предположим, что существуют пределы
на интервале (c,d). Предположим, что существуют пределы

Тогда несобственный интеграл  сходится, причём
сходится, причём
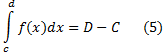
Равенство (5) вытекает из формулы Ньютона-Лейбница для обычных интегралов и соотношений (4).
Пример 1. Вычислим

Пример 2. Докажем???
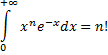

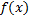 задана на полуинтервале
задана на полуинтервале 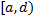 , где
, где 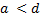 , а величина
, а величина 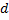 может быть как конечным числом, так и
может быть как конечным числом, так и  . Предположим, что
. Предположим, что 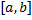 ,
, 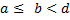 . Полагаем по определению
. Полагаем по определению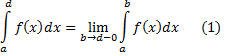
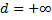 . Тогда
. Тогда 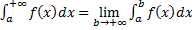
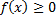 на полуинтервале
на полуинтервале  (см. рис. 1)
(см. рис. 1)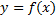
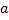

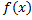 на самом деле интегрируема на отрезке
на самом деле интегрируема на отрезке 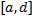 (это означает, в частности, что
(это означает, в частности, что 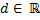 ), то коллизии обозначений не возникает -- несобственный интеграл в смысле (1) будет равен определенному интегралу функции
), то коллизии обозначений не возникает -- несобственный интеграл в смысле (1) будет равен определенному интегралу функции  на отрезке
на отрезке  , где
, где 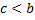 и
и  :
: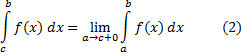
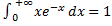 .
. сходятся, то для любых чисел k и m сходится также и интеграл
сходятся, то для любых чисел k и m сходится также и интеграл 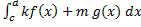 , и он равен
, и он равен 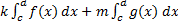 .
. такого, что
такого, что 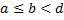 . Выберем точку
. Выберем точку 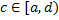 . Несобственный интеграл
. Несобственный интеграл  сходится в том и только том случае, если сходится несобственный интеграл
сходится в том и только том случае, если сходится несобственный интеграл 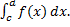 При этом условии имеет место равенство
При этом условии имеет место равенство
 -- первообразная непрерывной функции
-- первообразная непрерывной функции 
 сходится, причём
сходится, причём