Интеграл вида  называют интегралом с переменным верхним пределом.
называют интегралом с переменным верхним пределом.
Теорема. Пусть функция 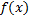 непрерывна на отрезке
непрерывна на отрезке 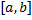 . Тогда
. Тогда  есть первообразная функции
есть первообразная функции 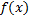 :
:

для любого 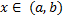 .
.
Доказательство. Пусть  . Тогда по теореме о среднем
. Тогда по теореме о среднем
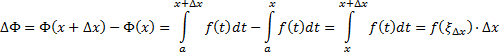
для некоторой точки  Следовательно,
Следовательно, 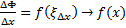 при
при 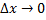 , ибо в этом случае
, ибо в этом случае  , а функция
, а функция 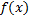 непрерывна.□
непрерывна.□
Формула Ньютона-Лейбница. Пусть  -- первообразная функции
-- первообразная функции 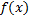 . Тогда
. Тогда
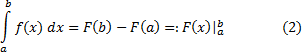
Доказательство. Для функции 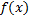 имеем в распоряжении две первообразных
имеем в распоряжении две первообразных  и
и  . По теореме о первообразных (см. § 10) найдется константа
. По теореме о первообразных (см. § 10) найдется константа  такая, что
такая, что
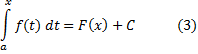
Подставим в соотношение (3) вместо 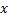 сначала
сначала 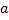 и получим
и получим 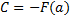 , а затем подставим
, а затем подставим  в (3) – получим
в (3) – получим
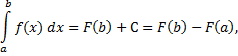
что и требовалось доказать.
Пример. 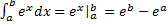 (см. пример вычисления площади в начале §14).
(см. пример вычисления площади в начале §14).
Замечание. Можно было бы определить логарифм так:

т.е. фактически как первообразную функции  , примимающую в точке 1 значение 0. Нетрудно доказать основное правило обращения с логарифмами:
, примимающую в точке 1 значение 0. Нетрудно доказать основное правило обращения с логарифмами:

Действительно,
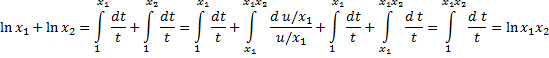
Тогда  – это такое число
– это такое число 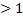 , что
, что 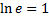 (т.е. площадь под гиперболой равна 1), а
(т.е. площадь под гиперболой равна 1), а 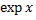 -- функция обратная к
-- функция обратная к  .
.
5 Замена переменной и интегрирование по частям в определённом интеграле
Замена переменной. Пусть 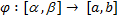 -- дифференцируемое отображение c непрерывной производной и такое, что
-- дифференцируемое отображение c непрерывной производной и такое, что 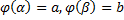 , а
, а 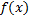 -- непрерывная функция, заданная на отрезке
-- непрерывная функция, заданная на отрезке 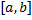 . Тогда
. Тогда

Доказательство. Пусть  -- первообразная функции
-- первообразная функции 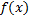 . Тогда по формуле замена переменной в неопределенном интеграле функция
. Тогда по формуле замена переменной в неопределенном интеграле функция  есть первообразная функции
есть первообразная функции  . Применим формулу Ньютона-Лейбница дважды:
. Применим формулу Ньютона-Лейбница дважды:

-- что и требовалось доказать. □
Пример 1. Вычислим площадь верхнего полукруга радиуса R.

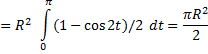
Интегрирование по частям. Пусть 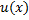 и
и  -- дифференцируемые функции на отрезке
-- дифференцируемые функции на отрезке 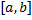 . Тогда
. Тогда
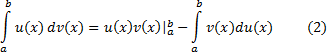
Доказательство. Соотношение 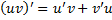 проинтегрируем от
проинтегрируем от 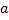 до
до  b получим
b получим 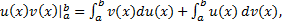 что эквивалентно (2).
что эквивалентно (2).
Пример 2. Вычислим

Заметим, что 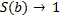 при условии
при условии 

 называют интегралом с переменным верхним пределом.
называют интегралом с переменным верхним пределом.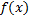 непрерывна на отрезке
непрерывна на отрезке 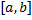 . Тогда
. Тогда  есть первообразная функции
есть первообразная функции 
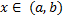 .
. . Тогда по теореме о среднем
. Тогда по теореме о среднем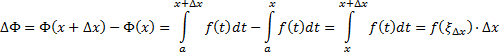
 Следовательно,
Следовательно, 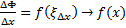 при
при 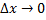 , ибо в этом случае
, ибо в этом случае  , а функция
, а функция  -- первообразная функции
-- первообразная функции 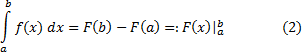
 такая, что
такая, что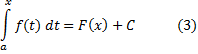
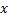 сначала
сначала 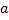 и получим
и получим 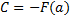 , а затем подставим
, а затем подставим  в (3) – получим
в (3) – получим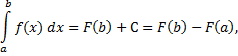
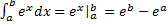 (см. пример вычисления площади в начале §14).
(см. пример вычисления площади в начале §14).
 , примимающую в точке 1 значение 0. Нетрудно доказать основное правило обращения с логарифмами:
, примимающую в точке 1 значение 0. Нетрудно доказать основное правило обращения с логарифмами:
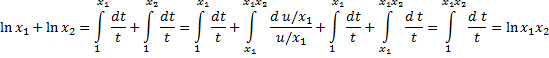
 – это такое число
– это такое число 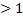 , что
, что 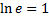 (т.е. площадь под гиперболой равна 1), а
(т.е. площадь под гиперболой равна 1), а 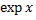 -- функция обратная к
-- функция обратная к  .
.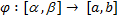 -- дифференцируемое отображение c непрерывной производной и такое, что
-- дифференцируемое отображение c непрерывной производной и такое, что 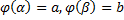 , а
, а 
 есть первообразная функции
есть первообразная функции  . Применим формулу Ньютона-Лейбница дважды:
. Применим формулу Ньютона-Лейбница дважды:

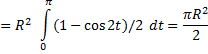
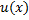 и
и  -- дифференцируемые функции на отрезке
-- дифференцируемые функции на отрезке 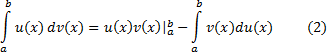
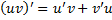 проинтегрируем от
проинтегрируем от  b получим
b получим 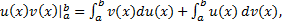 что эквивалентно (2).
что эквивалентно (2).
 при условии
при условии 



